Polinomo nuliai yra tikrosios, įsivaizduojamos ar sudėtingos reikšmės, kai vietoj kintamojo įterpiamas į daugianarį, rezultatas tampa nuliu (kaip ir pavadinimas rodo nulį). Polinomai naudojami kai kuriems realiame gyvenime vykstantiems fiziniams reiškiniams modeliuoti, jie labai praverčia matematiškai apibūdinant situacijas.

Polinomo nuliai yra visos x reikšmės, dėl kurių daugianomas lygus nuliui. Polinomo nuliai nurodo daugianario grafiko x atkarpas. Šiame straipsnyje kalbėsime apie daugianario nuliai, kaip juos rasti, faktoriaus teorema ir kt.

Turinys

• Kas yra polinomų nuliai?
• Polinominės formulės nuliai
• Kaip rasti polinomo nulį?
• Skirtas tiesiniam polinomui
• Kvadratiniam polinomui
• Kubiniam polinomui
• Faktoriaus teorema
• Nulių ir koeficiento santykis
• Kvadratinės lygties nulių ir koeficiento santykis
• Kubinės lygties nulių ir koeficiento santykis
• Sudarant lygtį su polinomo nuliais
• Nuliai polinomų grafike
• Pagrindinė tiesinės algebros teorema
• Šaknies įvairovė
• Straipsniai, susiję su polinomo nuliais
• Užduočių, susijusių su polinomo nuliais, pavyzdžiai
• Praktikos uždaviniai dėl polinomo nulių

Kas yra polinomų nuliai?

Polinomo P(x) atveju sakome, kad x = a yra daugianario nulis, jei P(a) = 0, ir visi tokie daugianario nuliai paprastai vadinami daugianario nuliais. Pavyzdžiui, apsvarstykite f(x) = 3x – 12. Dabar į daugianarį įdėkite x = 4, t.y., f(4) = 3×4 – 12 = 0. Taigi x = 4 yra polinomo f( x) = 3x – 12.

Pavyzdys: Jei f(x) = x ³ – 6x ² + 11x – 6, ar x = 1 yra nulis?

Sprendimas:

Norėdami patikrinti, ar jei x = 1 yra lygus f(x) = x nuliui³– 6x²+ 11x – 6 arba ne, įdėkite x = 1 in (x)

f(1) = (1)³– 6 × (1)²+ 11×(1) – 6

⇒ f(1) = 1–6 + 11–6 = 12–12 = 0

Taigi, x = 1 yra f(x) nulis.

Polinominės formulės nuliai

Ax + b formos tiesiniam polinomui jo nulis pateikiamas x = -b/a.

Ax formos kvadratiniam polinomui²+ bx + c, jo nulis gaunamas iš x = {- b ± √D}/2a, kur D yra diskriminantas, gautas iš b²– 4ac.

Kaip rasti polinomo nulį?

Įvairių tipų polinomų polinomo nulius galime rasti naudodami įvairius toliau aptartus metodus.

• Skirtas tiesiniam polinomui
• Kvadratiniam polinomui
• Kubiniam polinomui

Skirtas tiesiniam polinomui

Tiesinių polinomų atveju lengviausia rasti nulį. nes yra tik vienas nulis ir jį taip pat galima apskaičiuoti paprastu daugianario pertvarkymu po to, kai prilyginamas polinomas į 0.

Pavyzdžiui, raskite nulį tiesiniam daugianario f(x) = 2x – 7.

Sprendimas:

Norėdami rasti f(x) nulį, prilyginkite f(x) 0.

⇒ 2x – 7 = 0

⇒ 2x = 7

⇒ x = 7/2

Kvadratiniam polinomui

Yra įvairių būdų, kaip rasti kvadratinio daugianario šaknis arba nulius, pavyzdžiui, padalyti vidurinį terminą, kvadratinę formulę, kuri taip pat žinoma kaip Shree Dharacharya formulė, ir užbaigti kvadratą, kuris yra šiek tiek panašus į kvadratinę formulę, nes gaunama kvadratinė formulė. iš bendrosios kvadratinės lygties kvadrato užbaigimo.

Išmokti daugiau apie sprendžiant kvadratines lygtis arba daugianarius ir kaip juos išspręsti. Toliau pateikti pavyzdžiai išsamiai parodo kvadratinių polinomų nulių radimo metodą.

1 pavyzdys: Raskite nulius, kai P(x) = x ² + 2x – 15.

Atsakymas:

x²+ 2x – 15 = 0

⇒ x²+ 5x – 3x - 15 = 0

⇒ x(x + 5) – 3(x + 5) = 0

⇒ (x – 3) (x + 5) = 0

⇒ x = 3, -5

2 pavyzdys: Raskite nulius, kai P(x) = x ² – 16x + 64.

Atsakymas:

Vijay kino aktorius

x²– 16x + 64 = 0

Lyginant su kirviu²+ bx + c = 0,

gauname, a = 1, b = -16 ir c = 64.

Taigi,

⇒ x = 8, 8

Kubiniam polinomui

Norint rasti kubinio dydžio nulius, yra daug būdų, pavyzdžiui, racionalios šaknies teorema ir ilgas padalijimas kartu. Vienas iš būdų rasti kubinio ar bet kurio aukštesnio laipsnio daugianario šaknis yra toks:

1 žingsnis: Norėdami rasti galimas šaknis, naudokite racionalios šaknies teoremą. y., jei daugianomas turi racionaliąją šaknį, tai turi būti p/q padalijimas, kur p yra sveikojo skaičiaus konstanta, o q yra pagrindinis koeficientas.

2 žingsnis: Suradę vieną šaknį, padalykite daugianarį su tos šaknies suformuotu koeficientu, naudodami ilgąjį padalijimą, ir parašykite daugianarį kaip koeficiento ir dividendo sandaugą.

3 veiksmas: Jei koeficientas yra kvadratinė išraiška, išspręskite ją aukščiau nurodytais kvadratinių daugianarių metodais. Jei ne 2 laipsnio daugianario, kartokite 1 ir 2 veiksmus, kol koeficientas taps 2 laipsnio daugianario.

4 veiksmas: 3 žingsnio rezultatas – reikalingi koeficientai, o koeficientą prilyginę 0, galime rasti daugianario nulius.

Pavyzdys: Raskite kubinio daugianario p(x) = x nulius ³ + 2x ² – 5x – 6.

turi kitą java

Sprendimas:

p(x) = x³+ 2x²– 5x – 6

Kadangi p/q = -6

Pagal racionaliosios šaknies teoremą visos galimos racionalios polinomio šaknys yra p/q dalikliai.

Taigi, dalikliai = ±1, ±2, ±3, ±6

x = -1, p(x), gauname

p(-1) = (-1)³+ 2 (-1)²– 5(-1) – 6

⇒ p(-1) = -1 + 2 + 5 – 6 = 0

Taigi pagal faktoriaus teoremą x + 1 yra p(x) koeficientas.

Taigi, x³+ 2x²– 5x – 6 = (x+1)(x²+x – 6)

⇒ x³+ 2x²– 5x – 6 = (x+1)(x-2)(x+3)

Nulių atveju p(x) = 0,

P(x) nuliai yra x = -1, x = 2 ir x = -3.

Faktoriaus teorema

Dauginamo P(x) koeficiento teorema teigia, kad jei x =a yra P(X) nulis, jei f x – a yra P(x) koeficientas. y., abi šios sąlygos turėtų būti teisingos.

• Jei a yra P(x) nulis, tai x−a bus P(x) koeficientas
• Jei x−a yra P(x) koeficientas, tai a bus P(x) nulis

Tai galima patikrinti peržiūrėjus ankstesnius pavyzdžius. Faktoriaus teorema gali duoti įdomių rezultatų, kurie yra tokie:

1 rezultatas: Jei P(x) yra n laipsnio polinomas, o r yra P(x) nulis, tada P(x) galima parašyti tokia forma:

P(x) = (x – r) Q(x)

Kur Q(x) yra n-1 laipsnio daugianomas ir jį galima sužinoti padalijus P(x) su (x – r).

2 rezultatas: Jei P(x) = (x-r)Q(x) ir x = t yra Q(x) nulis, tai x = t taip pat bus P(x) nulis.

Norėdami patikrinti aukščiau nurodytą faktą,

Tarkime, t yra nulis Q(x), o tai reiškia, kad Q(t) = 0.

Žinome, kad r yra polinomo P(x) nulis, kur P(x) = (x – r) Q(x),

Taigi turime patikrinti, ar x = t taip pat yra P(x) nulis, įdėkime x = t į P(x)

⇒ P(t) = (t – r) Q(t) = 0

Taigi, x = t taip pat yra nulis P(x).

Vadinasi, įrodyta.

Nulių ir koeficiento santykis

Toliau aptariamas santykis tarp nulių ir kvadratinės bei kubinės lygties koeficiento.

Kvadratinės lygties nulių ir koeficiento santykis

Formos ax kvadratinei lygčiai²+ bx + c = 0, jei du kvadratinės lygties nuliai yra α ir β, tada

• Šaknies suma = α + β = -b/a
• Šaknų sandauga = α × β = c/a

Kubinės lygties nulių ir koeficiento santykis

Jei α, β ir γ yra kubinio daugianario ašies šaknis³+ bx²+ cx + d = 0, tada santykis tarp jo nulių ir koeficientų pateikiamas taip:

• a + b + c = -b/a
• α × β × γ= -d/a
• αβ + αγ + βγ = c/a

Sudarant lygtį su polinomo nuliais

• Kvadratinio daugianario, kurio nuliai α ir β, kvadratinis daugianomas gaunamas taip

x ² – (a + b)x + ab .

• Kubinio daugianario su trimis nuliais α, β ir γ kubinis daugianario dydis apskaičiuojamas taip

x ³ – (a + b + c )x ² + (ab + ag + bg)x – abg

Nuliai polinomų grafike

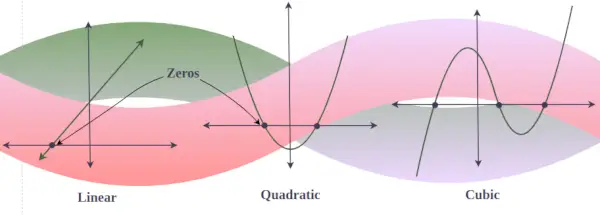
Bet kurio daugianario y = f(x) grafike tikrieji nuliai yra taškas, kuriame grafikas kerta arba liečia x ašį. (kaip grafikas su įsivaizduojamu nuliu niekada nekerta x ašies). Kitaip tariant, jei yra 3 realieji kubinio daugianario sprendiniai, tai to kubinio daugianario grafikas kerta x ašį tris kartus, bet jei kurio nors kubinio daugianario yra tik vienas tikrasis sprendinys, tai grafikas tik pjauna x ašį. kartą.

Pagrindinė tiesinės algebros teorema

Jei P(x) yra n laipsnio daugianomas, P(x) turės tiksliai n nulių, kai kurie iš jų gali pasikartoti.

skaityti iš csv java

Tai reiškia, kad jei išvardysime visus nulius ir kiekvieną išvardysime k kartų, kai k yra jo dauginys. Sąraše turėsime lygiai n skaičių. Tai gali būti naudinga, nes gali susidaryti supratimą, kiek nulių turi būti daugianario. Taigi, pasiekę reikiamą nulių skaičių, galime nustoti ieškoti nulių.

Šaknies įvairovė

Tarkime, kad turime daugianarį P(x) = 0, kuris susideda į

P(x) = (x – r) ^k (x – a) ^m

Jei r yra daugianario nulis, o jo nario rodiklis, sudaręs šaknį, yra k, tada sakome, kad r daugyba k . Dažnai vadinami nuliai, kurių daugyba yra 1 paprastas nuliai ir nuliai, kurių daugyba yra 2, vadinami dvigubomis daugianario šaknimis.

Pavyzdys: P(x) yra 5 laipsnio daugianario, kuris buvo koeficientas jums. Išvardykite šaknis ir jų įvairovę.

P(x) = 5x ⁵ -20 kartų ⁴ +5x ³ +50 kartų ² −20x−40 = 5(x+1) ² (x–2) ³

Sprendimas:

Duota, P(x) = 5 (x+1)²(x–2)³

⇒ P(x) = 5(x+1)(x+1)(x+1)(x−2)(x−2)

Norėdami rasti nulius, P(x) = 0

⇒ x = -1, -1, 2, 2, 2

Atkreipkite dėmesį, kad -1 įvyksta du kartus kaip nulis, todėl jo daugyba yra 2, o nulio 2 daugyba yra 3.

Straipsniai, susiję su polinomo nuliais

• Polinomas
• Kvadratinės lygties šaknys
• Algebrinė išraiška

Užduočių, susijusių su polinomo nuliais, pavyzdžiai

1 uždavinys: Atsižvelgiant į tai, kad x = 2 yra P(x) = x nulis ³ +2x ² −5x−6. Raskite kitus du nulius.

Sprendimas:

Iš pagrindinės teoremos, kurią išnagrinėjome anksčiau, galime pasakyti, kad P(x) turės 3 nulius, nes tai yra trijų laipsnių daugianario. Vienas iš jų yra x = 2.

Taigi galime perrašyti P(x),

P(x) = (x – 2) Q(x)

Norėdami rasti kitus du nulius, turime išsiaiškinti Q (x).

Q(x) galima sužinoti padalijus P(x) iš (x-2).

Po padalijimo Q(x) išeina kaip

Q(x) = x²+ 4x + 3

Iš to galima sužinoti likusius du nulius,

Q(x) = x²+ 3x + x + 3

⇒ x(x + 3) + 1 (x + 3)

⇒ (x + 1) (x + 3)

Q(x) = 0,

x = -1, -3

Taigi kiti du nuliai yra x = -1 ir x = -3.

2 uždavinys: Atsižvelgiant į tai, kad x = r yra daugianario nulis, išsiaiškinkite kitus daugianario nulius.

P(x) = x ³ -6x ² −16x; r = −2

Sprendimas:

Mes žinome, kad x = -2 yra nulis,

Taigi, P(x) galima perrašyti kaip P(x) = (x + 2) Q(x) {naudojant padalijimo algoritmą}

Dabar norėdami rasti Q(x), darome tą patį, ką darėme ankstesniame klausime, padalijame P(x) su (x + 2).

Mes gauname,

Q(x) = x²– 8x

Dabar norėdami rasti kitus du nulius, koeficientą Q(x)

Q(x) = x (x – 8) = 0

Taigi, nuliai yra x = 0, 8.

Taigi, mes turime tris nulius, x = -2, 0, 8.

3 uždavinys: Raskite polinomo, 4x, nulius ³ -3x ² -25x-6 = 0

kas yra dviguba java

Sprendimas:

Triukas išspręsti daugianario lygtis su 3 laipsniu,

Raskite mažiausią sveikąjį skaičių, kuris gali sudaryti daugianario reikšmę 0, pradėti nuo 1, -1, 2 ir pan.

nustatome, kad jei x = -2, išraiškos reikšmė yra lygi nuliui.

Taigi viena iš šaknų yra -2.

Pagal faktoriaus teoremą, jei a yra vienas iš daugianario nulių, tai (x-a) yra duotojo daugianario koeficientas.

Taigi po šio {x – (-2)} = (x+2) yra koeficientas pof virš daugianario.

Gauname kvadratinę lygtį ir jau yra nuliai.

(4x²-11x-3) (x+2) = 0

Paskaičiuokite kvadratinę lygtį,

(4x²-12x+x-3)(x+2) = 0

[4x(x-3)+1(x-3)](x+2) = 0

(4x+1)(x-3)(x+2) = 0

x = -2, x = 3, x = -1/4

4 uždavinys: Raskite polinomo, 4x, nulius ⁶ – 16 kartų ⁴ = 0

Sprendimas:

Polinomas turi iki 6 laipsnio, vadinasi, egzistuoja 6 daugianario nuliai.

4x⁴(x²-4) = 0

4x⁴(x²-2²) = 0

4x⁴[(x+2)(x-2)] = 0

Todėl x = 0, 0, 0, 0, 2, -2

ascii lentelė java

5 uždavinys: Raskite daugianario funkcijos f(x) = x nulius ³ – 2x ² – 5x + 6

Sprendimas:

Norėdami rasti šio daugianario nulius, nustatome f(x) = 0 ir išsprendžiame x:

f(x) = x³– 2x²– 5x + 6 = 0

Kadangi d/a = 6

Pagal racionaliosios šaknies teoremą visos galimos racionalios polinomio šaknys yra

d/a dalikliai = ±1, ±2, ±3, ±6

x = 1, p(x), gauname

f(1) = (1)³– 2 straipsnio 1 dalis²– 5 straipsnio 1 dalis – 6 dalis

f(-1) = 1 – 2 – 5 + 6 = 0

Taigi pagal faktoriaus teoremą x – 1 yra p(x) koeficientas.

Taigi, x³+ 2x²– 5x – 6 = (x-1) (x²-x - 6)

x³+ 2x²– 5x – 6 = (x-1) (x+2) (x-3)

Nulių atveju p(x) = 0,

P(x) nuliai yra x = 1, x = -2 ir x = 3.

Praktikos uždaviniai dėl polinomo nulių

1. Raskite visus polinomo f(x) = x nulius ³ – 6x ² + 11x – 6

2. Nustatykite visus daugianario g(x) = 2x nulius ⁴ – 7x ³ + 3x ² + 4x – 4

3. Raskite daugianario h(x) = x nulius ⁵ – 3x ⁴ + 2x ³ – 6x ² + x + 2

4. Nustatykite visus daugianario nulius p(x) = 3x ⁴ – 16 kartų ³ + 18x ² + 16x – 12.

DUK apie polinomo nulius

Kas yra polinomo nuliai?

Tokios tikrosios reikšmės, nes daugianario reikšmė tampa 0, ty jei p(x) yra daugianario, o p(a) = 0, tai x = a yra p(x) nulis.

Kaip rasti polinomo nulius?

Yra įvairių metodų, skirtų įvairiems įvairiems daugianariams rasti nulius, pvz., kvadratinį vidurio terminą ir kvadratinę formulę. Linijiniam, paprastam kintamųjų ir kubiniam pertvarkymui naudojame racionalios šaknies teoremos, ilgosios dalybos, faktoriaus teoremos ir liekanos teoremos derinį.

Ar polinome gali būti daugiau nei vienas nulis?

Taip, daugianario gali būti daugiau nei vienas nulis, iš tikrųjų n laipsnių daugianario gali būti daugiausia n tikrų nulių.

Kas yra polinomo nulio daugyba?

Faktorizacijos procese vienas daugianario veiksnys arba vienas nulis, po to kelis kartus atsirado koeficientas arba nulis, tai vadinama tos šaknies dauginimu.

Kas yra pagrindinė algebros teorema?

Pagrindinė algebros būsenų teorema Jei P(x) yra n laipsnio polinomas, tai P(x) turės lygiai n nulių, kai kurie iš jų gali pasikartoti.

Ar polinomas, kurio laipsnis n, visada turi n tikrų šaknų?

Ne, daugianario su n laipsniu ne visada yra n realių šaknų, nes kai kurios šaknys gali būti įsivaizduojami arba kompleksiniai skaičiai.

Kas yra nulinio polinomo laipsnis?

Nulinio daugianario laipsnis lygus nuliui.