Z-BALAS STATISTIKOJE - DUOMENŲ MOKSLAS

Z-balas statistikoje yra matavimas, kiek standartinių nuokrypių duomenų taškas turi nuo skirstinio vidurkio. Raskime z balą statistikoje. Z-balas 0 rodo, kad duomenų taško balas yra toks pat kaip vidutinis balas. Teigiamas z balas rodo, kad duomenų taškas yra didesnis už vidurkį, o neigiamas z balas rodo, kad duomenų taškas yra žemesnis už vidurkį.

Z balo apskaičiavimo formulė yra tokia: z = (x – μ)/ p

Kur:

x: yra testo vertė
m: yra vidurkis
adresu: yra standartinė vertė

Šiame straipsnyje aptarsime šias sąvokas:

Turinys

Kas yra Z-Score?
Kaip apskaičiuoti Z balą?
Z-score charakteristikos
Apskaičiuokite nuokrypius naudodami Z balo reikšmę
Z-Score įdiegimas Python
Z-Score taikymas
Z balai ir standartinis nuokrypis
Kodėl Z balai vadinami standartiniais balais?

Kas yra Z-Score?

Z balas, dar žinomas kaip standartinis balas, parodo duomenų taško nuokrypį nuo vidurkio, išreiškiant jį standartiniais nuokrypiais, viršijančiais arba žemiau vidurkio. Tai suteikia mums supratimą, kiek duomenų taškas yra toli nuo vidurkio. Taigi Z balas matuojamas standartiniu nuokrypiu nuo vidurkio. Pavyzdžiui, Z balas 2 rodo, kad vertė yra 2 standartiniais nuokrypiais nuo vidurkio. Norėdami naudoti z balą, turime žinoti populiacijos vidurkį (μ) ir populiacijos standartinį nuokrypį (σ).

Z balo formulė

Z balą galima apskaičiuoti naudojant šią formulę.

z = (X – μ) / p

kur,

z = Z balas
X = elemento vertė
μ = gyventojų vidurkis
σ = populiacijos standartinis nuokrypis

Kaip apskaičiuoti Z balą?

Mums pateikiamas populiacijos vidurkis (μ), populiacijos standartinis nuokrypis (σ) ir pastebėta reikšmė (x) problemos teiginyje, pakeičiant tą patį Z balo lygtyje, gaunama Z balo reikšmė. Priklausomai nuo to, ar nurodytas Z balas yra teigiamas, ar neigiamas, galime naudoti teigiama Z lentelė arba neigiama Z lentelė galima rasti internete arba priede esančio statistikos vadovėlio gale.

1 pavyzdys:

Laikote GATE egzaminą ir įvertinate 500. Vidutinis GATE balas yra 390, o standartinis nuokrypis yra 45. Kaip gerai įvertinote testą, palyginti su vidutiniu testo dalyviu?

Sprendimas:

Šie duomenys yra lengvai prieinami aukščiau pateiktame klausimo teiginyje

Neapdorotas balas / pastebėta vertė = X = 500

Vidutinis balas = μ = 390

Standartinis nuokrypis = σ = 45

Taikant z balo formulę,

z = (X – μ) / p

z = (500–390) / 45

z = 110 / 45 = 2,44

Tai reiškia, kad jūsų z balas yra 2.44 .

Kadangi Z balas yra teigiamas 2,44, naudosime teigiamą Z lentelę.

Dabar pažvelkime į Z lentelė (CC-BY), kad sužinotumėte, kokius balus surinkote, palyginti su kitais testo dalyviais.

Vadovaukitės toliau pateikta instrukcija, kad rastumėte tikimybę iš lentelės.

Čia z balas = 2,44, kurios i rodo, kad duomenų taškas yra 2,44 standartinio nuokrypio didesnis už vidurkį.

Pirmiausia pažymėkite pirmuosius du skaitmenis 2,4 Y ašyje.
Tada išilgai X ašies žemėlapis 0,04
Sujunkite abi ašis. Šių dviejų sankirta suteiks jums kaupiamąją tikimybę, susijusią su jūsų ieškoma Z balo reikšme

[Ši tikimybė reiškia plotą po standartine normaliąja kreive į kairę nuo Z balo]

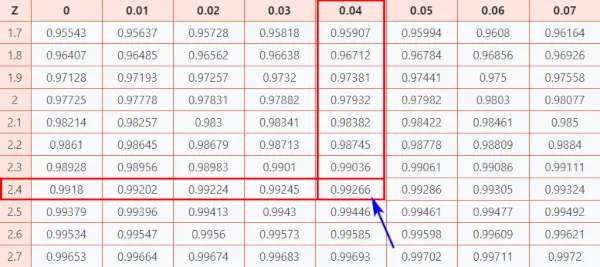
Normalaus paskirstymo lentelė

Dėl to jūs gausite galutinę vertę, kuri yra 0,99266 .

Dabar turime palyginti, kaip mūsų pradinis 500 balų GATE egzaminas yra lyginamas su vidutiniu partijos balu. Norėdami tai padaryti, turime paversti sukauptą tikimybę, susietą su Z balu, į procentinę reikšmę.

0,99266 × 100 = 99,266 %

Galiausiai galite pasakyti, kad pasirodėte gerai nei beveik 99 % kitų egzaminuotojų.

2 pavyzdys : Kokia tikimybė, kad studentas surinks balus nuo 350 iki 400 (kai vidutinis balas μ yra 390 ir standartinis nuokrypis σ 45)?

Sprendimas:

Minimalus rezultatas = X₁= 350

Maksimalus rezultatas = X₂= 400

Taikant z balo formulę,
java nepakeičiamas sąrašas

Su₁= (X1 – m) / p

Su₁= (350–390) / 45

Su₁= -40 / 45 = -0,88

Su₂= (X₂– m) / p

z2 = (400–390) / 45

Su₂= 10 / 45 = 0,22

Kadangi z1 yra neigiamas, turėsime žiūrėti į neigiamą Z lentelė ir rasti, kad kumuliacinė tikimybė p1, pirmoji tikimybė, yra 0,18943 .

Su₂yra teigiamas, todėl naudojame teigiamą Z lentelę, kuri duoda kaupiamąją tikimybę p₂apie 0,58706 .

Galutinė tikimybė apskaičiuojama iš p atėmus p1₂:

p = p₂– p₁

p = 0,58706 – 0,18943 = 0,39763

Tikimybė, kad studentas surinks nuo 350 iki 400 balų yra 39,763 % (0,39763 * 100).

Z-score charakteristikos

Z balo dydis parodo, kaip toli duomenų taškas yra nuo standartinių nuokrypių vidurkio.
Elementas, kurio z balas yra mažesnis nei 0, reiškia, kad elementas yra mažesnis už vidurkį.
Z balai leidžia palyginti skirtingų skirstinių duomenų taškus.
Elementas, kurio z balas didesnis nei 0, reiškia, kad elementas yra didesnis už vidurkį.
Elementas, kurio z balas lygus 0, reiškia, kad elementas yra lygus vidurkiui.
Elementas, kurio z balas lygus 1, reiškia, kad elementas yra 1 standartiniu nuokrypiu didesnis už vidurkį; z balas, lygus 2, 2 standartiniai nuokrypiai, didesni už vidurkį ir pan.
Elementas, kurio z balas lygus -1, reiškia, kad elementas yra 1 standartiniu nuokrypiu mažesnis už vidurkį; z balas, lygus -2, 2 standartiniai nuokrypiai mažesni už vidurkį ir pan.
Jei elementų skaičius tam tikroje aibėje yra didelis, tada apie 68 % elementų z balas yra nuo -1 iki 1; apie 95 % z balas yra tarp -2 ir 2; apie 99 % z balas yra nuo -3 iki 3. Tai žinoma kaip empirinė taisyklė ir nurodo procentinę duomenų dalį, kuri yra tam tikri standartiniai nuokrypiai nuo vidurkio normaliame skirstinyje, kaip parodyta paveikslėlyje toliau.

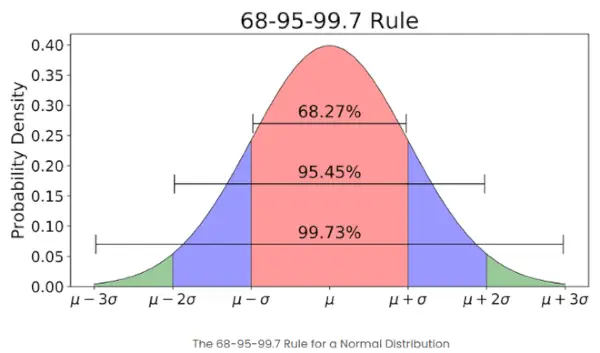
Empirinė normaliojo skirstinio taisyklė

Apskaičiuokite nuokrypius naudodami Z balo reikšmę

Duomenų nuokrypius galime apskaičiuoti naudodami duomenų taškų z balo reikšmę. Išskirtinių duomenų taško įvertinimo veiksmai yra tokie:

Iš pradžių renkame duomenų rinkinį, kuriame norime matyti išskirtines vertes
Apskaičiuosime duomenų rinkinio vidurkį ir standartinį nuokrypį. Šios vertės bus naudojamos kiekvieno duomenų taško z balo reikšmei apskaičiuoti.
Apskaičiuosime kiekvieno duomenų taško z balo reikšmę. z balo reikšmės apskaičiavimo formulė bus tokia pati kaip
Z = frac{{X – mu}}{{sigma}}
kur X bus duomenų taškas, μ – duomenų vidurkis, o σ – standartinis duomenų rinkinio nuokrypis.
Nustatysime ribinę z balo vertę, po kurios duomenų taškas gali būti laikomas išskirtiniu. Ši ribinė vertė yra hiperparametras, kurį nusprendžiame atsižvelgdami į savo projektą.
Duomenų taškas, kurio z balo reikšmė yra didesnė nei 3, reiškia, kad duomenų taškas nepriklauso 99,73 % duomenų rinkinio taškui.
Bet kuris duomenų taškas, kurio z balas yra didesnis už mūsų nustatytą ribinę vertę, bus laikomas išskirtiniu.

Patikrinti: Z balas už pašalinių ribų aptikimą

Z-Score įdiegimas Python

Galime naudoti Python duomenų rinkinio duomenų taškų z balo reikšmei apskaičiuoti. Be to, duomenų rinkinio vidurkiui ir standartiniam nuokrypiui apskaičiuoti naudosime numpy biblioteką.

jei kitaip jei kitaip jei java

Python3

 import numpy as np def calculate_z_score(data): # Mean of the dataset mean = np.mean(data) # Standard Deviation of tha dataset std_dev = np.std(data) # Z-score of tha data points z_scores = (data - mean) / std_dev return z_scores # Example dataset dataset = [3,9, 23, 43,53, 4, 5,30, 35, 50, 70, 150, 6, 7, 8, 9, 10] z_scores = calculate_z_score(dataset) print('Z-Score :',z_scores) # Data points which lies outside 3 standard deviatioms are outliers # i.e outside range of99.73% values outliers = [data_point for data_point,  z_score in zip(dataset, z_scores) if z_score>3] print(f'
Duomenų rinkinio nuokrypiai yra {outliers}')>

Išvestis:

Z balas : [-0,7574907 -0,59097335 -0,20243286 0,35262498 0,6301539 -0,72973781
-0,70198492 -0,00816262 0,13060185 0,54689523 1,10195307 3,32218443
-0,67423202 -0,64647913 -0,61872624 -0,59097335 -0,56322046]
Nukrypimai duomenų rinkinyje yra [150]

Z-Score taikymas

Z balai dažnai naudojami funkcijų mastelio keitimui, siekiant sujungti skirtingas funkcijas į bendrą skalę. Funkcijų normalizavimas užtikrina, kad jų vidurkis ir vienetų dispersija būtų nulinė, o tai gali būti naudinga tam tikriems mašininio mokymosi algoritmams, ypač tiems, kurie priklauso nuo atstumo matavimų.
Z balai gali būti naudojami duomenų rinkinio nuokrypiams nustatyti. Duomenų taškai, kurių Z balai viršija tam tikrą ribą (paprastai 3 standartiniai nuokrypiai nuo vidurkio), gali būti laikomi išskirtiniais.
Z balai gali būti naudojami anomalijų aptikimo algoritmuose, siekiant nustatyti atvejus, kurie labai skiriasi nuo numatomo elgesio.
Z balai gali būti taikomi norint transformuoti iškreiptus skirstinius į normalesnius skirstinius.
Dirbant su regresijos modeliais, galima analizuoti likučių Z balus, siekiant patikrinti homoskedastiškumą (pastovią likučių dispersiją).
Z balai gali būti naudojami nustatant funkcijų mastelį, žiūrint į jų standartinius nuokrypius nuo vidurkio.

Z balai ir standartinis nuokrypis

Z- Rezultatas	Standartinis nuokrypis
Paverskite neapdorotus duomenis į standartizuotą skalę.	Matuoja verčių rinkinio kitimo arba sklaidos dydį.
Palengvina skirtingų duomenų rinkinių verčių palyginimą, nes jie atima pradinius matavimo vienetus.	Standartinis nuokrypis išlaiko pradinius matavimo vienetus, todėl jis mažiau tinkamas tiesioginiam duomenų rinkinių su skirtingais vienetais palyginimui.
Nurodykite, kiek duomenų taškas yra toli nuo vidurkio pagal standartinius nuokrypius, nurodant duomenų taško santykinės padėties skirstinyje matą.	Išreiškiama tais pačiais vienetais kaip ir pirminiai duomenys, nurodant absoliutų verčių pasiskirstymą apie vidurkį

Patikrinti: Z balų lentelė

Kodėl Z balai vadinami standartiniais balais?

Z balai taip pat žinomi kaip standartiniai balai, nes jie standartizuoja atsitiktinio dydžio reikšmę. Tai reiškia, kad standartizuotų balų sąrašo vidurkis yra 0, o standartinis nuokrypis – 1,0. Z-balai taip pat leidžia palyginti skirtingų tipų kintamųjų balus. Taip yra todėl, kad jie naudoja santykinę padėtį, kad sulygintų balus iš skirtingų kintamųjų ar skirstinių.

Z balai dažnai naudojami lyginant kintamąjį su standartiniu normaliuoju skirstiniu (su μ = 0 ir σ = 1).

Z-Score statistikoje – DUK

Kokia yra teigiamų ir neigiamų Z balų reikšmė?

Teigiami Z balai rodo vertes, viršijančias vidurkį, o neigiamos Z balai rodo reikšmes, žemesnes už vidurkį. Ženklas atspindi nukrypimo nuo vidurkio kryptį.

Ką reiškia 0 Z balas?

0 Z balas rodo, kad duomenų taško reikšmė tiksliai atitinka duomenų rinkinio vidurkį. Tai rodo, kad duomenų taškas nėra nei didesnis, nei žemiau vidurkio.

Kokia yra 68-95-99.7 taisyklė, susijusi su Z balais?

68-95-99.7 taisyklė, taip pat žinoma kaip empirinė taisyklė, teigia, kad:

Apie 68 % duomenų patenka į 1 standartinį nuokrypį nuo vidurkio.
Apie 95% patenka į 2 standartinius nuokrypius.
Apie 99,7% patenka į 3 standartinius nuokrypius.

Ar Z balai gali būti naudojami nenormaliems skirstiniams?

Z balai yra pagrįsti prielaida, kad duomenys atitinka normalųjį pasiskirstymą. Tačiau praktiškai Z balai yra naudingi duomenims, kurie atitinka normalų pasiskirstymą. Nors Z balai gali būti skaičiuojami bet kokiam pasiskirstymui, jų aiškinimas tampa mažiau patikimas ir aiškus, kai kalbama apie nenormaliai paskirstytus duomenis.

Kaip Z-Scores galima pritaikyti realiose situacijose?

„Z-Scores“ turi įvairių pritaikymų, pavyzdžiui, finansų portfelio analizei, švietimui standartizuotiems tyrimams, sveikatos klinikiniams vertinimams ir kt. Jie suteikia standartizuotą duomenų palyginimo ir interpretavimo priemonę.