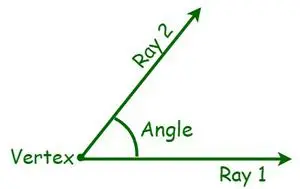
Geometrijoje kampas yra esminis geometrinės formos matas. Kampas apibrėžiamas kaip sukimosi apie dviejų tiesių arba plokštumų susikirtimo tašką laipsnis, kurio reikia, kad viena sutaptų su kita. Yra įvairių tipų kampai, pagrįsti kampo matavimu. Jis matuojamas laipsniais arba radianais. Kampas yra forma, kurią sudaro dvi linijos arba spinduliai, kurie skiriasi nuo bendro taško, vadinamo viršūne. Kai susikerta du spinduliai, t.y., kai pustiesės projektuojamos su bendru galiniu tašku, susidaro kampas. Dabar bendrieji galiniai taškai vadinami viršūnėmis, o spinduliai vadinami rankomis.
Kampų tipai

- Ūminis kampas: Smailusis kampas yra kampas, didesnis nei 0 laipsnių ir mažesnis nei 90 laipsnių, t. y. jis svyruoja nuo 0° iki 90° (abu išskyrus).
- Tiesus kampas: Status kampas vadinamas kampu, kuris matuojamas tiksliai 90 laipsnių.
- Bukas kampas: Bukas kampas yra kampas, didesnis nei 90 laipsnių ir mažesnis nei 180 laipsnių, t. y. jis svyruoja nuo 90° iki 180° (abu išskirtiniai).
- Tiesus kampas: Tiesus kampas vadinamas kampu, kuris matuojamas tiksliai 180 laipsnių.
- Reflekso kampas: Reflekso kampas yra kampas, didesnis nei 180 laipsnių ir mažesnis nei 360 laipsnių, ty jis svyruoja nuo 180° iki 360° (abu išskirtiniai).
- Visas kampas arba visas pasukimas: Visas kampas vadinamas kampu, kuris matuojamas tiksliai 360 laipsnių.
Taip pat yra ir kitų tipų kampų, tokių kaip papildomi kampai, papildomi kampai ir gretimi bei negretimi kampai.
- Papildomi kampai: Sakoma, kad du kampai papildo vienas kitą, jei jų suma yra stačiakampis, ty 90°.
- Papildomi kampai: Sakoma, kad du kampai yra papildomi, jei jų suma lygi 180°.
- Gretimi kampai: Sakoma, kad du kampai yra gretimi, jei jie turi bendrą viršūnę ir bendrą šaką.
- Ne gretimi kampai: Sakoma, kad du kampai yra negretimi, jei jie neturi bendros viršūnės ir bendros rankos.
Kampų radimo formulė
Kampui rasti yra įvairių formų; kai kurios iš jų yra centrinio kampo formulė, dvigubo kampo formulė, pusės kampo formulė, sudėtinio kampo formulė, vidinio kampo formulė ir kt.
- Apskritime sudarytos atkarpos kampui nustatyti naudojame centrinio kampo formulę.
- Trūkstamam daugiakampio kampui nustatyti naudojame vidinių kampų sumos formulę.
- Norėdami rasti trūkstamą stačiakampio trikampio kampą, naudojame trigonometrinius santykius.
- Norėdami rasti trūkstamą nestačiojo kampo trikampio kampą, naudojame sinusų arba kosinusų dėsnį.
Formulės pavadinimas | Formulė | Kaip rasti nežinomą kampą? |
|---|---|---|
| Centrinio kampo formulė | θ =(s × 360°)/2prČia s yra lanko ilgis, o r yra apskritimo spindulys | Pakeiskite lanko ilgio ir apskritimo spindulio reikšmes, kad nustatytumėte apskritime sudarytos atkarpos kampą. |
| Vidaus kampų sumos formulė | 180° (n-2)Čia n yra daugiakampio kraštinių skaičius | Norėdami nustatyti nežinomą daugiakampio vidinį kampą, pirmiausia pagal šią formulę apskaičiuokite visų vidinių kampų sumą ir iš rezultato atimkite visų žinomų kampų sumą. |
| Trigonometriniai santykiai | sin θ = priešinga pusė/hipotenuzėcos θ = gretima pusė/hipotenuzėtan θ = priešinga pusė/gretima pusė | Atsižvelgdami į dvi stačiakampio trikampio kraštines, pasirinkite vieną iš šių trigonometrinių koeficientų, kad surastumėte nežinomą kampą. Jungtinių Valstijų kiek miestų |
| Sinuso dėsnis | a/sin A = b/sin B = c/sin CČia A, B ir C yra vidiniai trikampio kampai, o a, b ir c yra jų atitinkamos priešingos kraštinės. | Kai žinome dvi kraštines ir neįtrauktą kampą (arba) du kampus ir neįtrauktąją kraštinę, tada nežinomiems trikampio kampams nustatyti galima naudoti sinusų dėsnį. |
| Kosinusų dėsnis | a2= b2+ c2– 2bc cos Ab2= c2+ a2– 2ca cos Bc2= a2+ b2– 2ab cos CČia A, B ir C yra vidiniai trikampio kampai, o a, b ir c yra jų atitinkamos priešingos kraštinės. | Kai žinome tris kraštines (arba) dvi kraštines ir įskaitytąjį kampą, tada nežinomiems trikampio kampams nustatyti galima naudoti kosinusų dėsnį. |
Klausimų pavyzdžiai
1 klausimas: raskite kampą nurodyto trikampio viršūnėje B, naudodami vieną iš trigonometrinių kampų nustatymo formulių.

Sprendimas:
Atsižvelgiant į
BC = 3 vienetai = gretima θ pusė.
AC = 4 vienetai = priešinga θ pusė.
Šiuo atveju žinome ir priešingą, ir gretimą θ puses. Taigi, norėdami rasti θ, galime naudoti liestinės formulę.
⇒ įdegis θ = priešinga pusė/gretima pusė
⇒ įdegio θ = 4/3
⇒ θ = įdegis-1(4/3) ⇒ θ = 53,1°
Vadinasi, kampas viršūnėje B yra 53,1°.
2 klausimas: suraskite kampus viršūnėse X ir Y, jei ∠Z = 35° ir x = 3 coliai, y = 8 coliai ir z = 3,5 colio.

Sprendimas:
Atsižvelgiant į
∠Z = 35° ir x = 6 coliai, y = 3 coliai ir z = 3,5 colio
Kadangi žinome visas tris puses ir kampą, galime naudoti sinuso taisyklės formulę.
Iš sinuso taisyklės formulės turime
x/sin X = y/sin Y = z/sin Z
Dabar
y/sin Y = z/sin Z
⇒ 3/sin Y = 3,5/sin 35°
⇒ 3/be Y = 3,5/0,574 {Kadangi sin 35° = 0,574}
⇒ sin Y = 3 × (0,574/3,5) = 0,492
⇒ ∠Y = nuodėmė−1(0,492) = 29,47°
Žinome, kad trijų trikampio kampų suma yra 180°.
⇒ ∠X + ∠Y + ∠Z = 180°
⇒ ∠X + 29,47° + 35° = 180°
⇒ ∠X = 180° – 64,47° = 115,53°
Vadinasi, ∠X = 115,53° ir ∠Y = 29,47°.
3 klausimas: Apskaičiuokite penktąjį penkiakampio vidinį kampą, jei keturi jo vidiniai kampai yra 110°, 85°, 136° ir 105°.
Sprendimas:
Penkiakampio kraštinių skaičius (n) = 5.
Dabar visų penkių penkiakampio vidinių kampų suma = 180 (n -2)°
= 180 (5–2)° = 540°.
Duotų 4 vidinių kampų suma = 110°+ 85°+ 136°+ ir 105°= 436°.
Taigi, penktasis vidinis kampas = 540° – 436° = 104°
Taigi penktasis vidinis penkiakampio kampas yra 104°.
4 klausimas: nustatykite y reikšmę ir kampų matą duotame paveiksle.

Sprendimas:
Iš pateikto paveikslo matome, kad (4y – 6)° ir (3y + 5)° yra vienas kitą papildantys kampai, t. y. (4y – 6)° ir (3y + 5)° suma yra 90 °.
⇒ (4y – 6)° + (3m + 5)° = 90°
⇒ (7y – 1)° = 90°
⇒ 7y = 90° + 1° = 91°
⇒ y = 91°/7 = 13°
Dabar (4 m – 6)° = (4 × 13 – 6)° = (52–6)° = 46°
(3 m. + 5)° = (3 × 13 + 5)° = (39 + 5)° = 44°
5 klausimas: naudodamiesi viena iš kampų radimo formulių raskite kampą, esantį duoto trikampio viršūnėje Q.

Sprendimas:
Pateikta, p = QR = 6 cm, q = PR = 9 cm ir r = PQ = 7 cm.
Kadangi žinome visas tris puses ir kampą, kampo viršūnei Q rasti galime naudoti kosinuso taisyklės formulę.
⇒ q2= p2+ r2– 2pr cos Q
⇒ 92= 62+ 72– 2(6)(7), nes Q
⇒ 81 = 36 + 49 - 84 cos Q
⇒ 81 = 85–84 cos Q
⇒84 cos Q = 81–85
⇒ 84 cos Q = -4
⇒ cos Q = -4/84 = -1/21
⇒ ∠Q = cos-1(-1/21) = 92,72°
Vadinasi, kampas viršūnėje Q, ∠Q = 92,72°.
6 klausimas: Apskaičiuokite atkarpos, sudarytos apskritime, kampą, jei lanko ilgis yra 12π, o spindulys yra 9 cm.
Sprendimas:
Atsižvelgiant į
Lanko ilgis = 12π
Spindulys (r) = 9 cm
Dabar kampo formulė yra tokia:
⇒ θ = (s × 360°)/2pr
⇒ θ = (12π × 360°) / (2π × 5)
⇒ θ =12 × 360°/10
⇒ θ = 240°
Taigi kampas yra 240°.
„Java“ eilutės žetonų priemonė
