Sferos tūris yra skysčio kiekis, kurį gali laikyti rutulys. Sferos formulės tūris pateikiamas kaip 4/3πr³. Tai erdvė, kurią užima sfera 3-matėje erdvėje. Jis matuojamas vienetais³y. m³, cm³ir tt Sfera yra trimatis kietas objektas, kurio geometrija yra apvali.

Sferos tūris – tai bendra erdvė, kurią užima rutulio paviršius, ir ji yra proporcinga sferos spindulio kubui. Šiame straipsnyje mes išsamiai sužinosime apie sferos tūrį, sferos tūrį, formulės tūrį, sferos formulės pavyzdžius ir kitus.

• Kas yra sferos tūris?
• Sferos formulės tūris
• Kietos sferos tūris
• Tuščiavidurės sferos tūris
• Sferos formulės išvedimo tūris
• Kaip apskaičiuoti sferos tūrį?

Kas yra sferos tūris?

Sferos tūris yra erdvės, kurią ji užima joje, kiekis. Sfera yra trimatė apvali kieta forma, kurios visi taškai ant jo paviršiaus yra vienodai nutolę nuo centro. Fiksuotas atstumas yra rutulio spindulys, o fiksuotas taškas yra sferos centras. Apsukus ratą pastebėsime formos pasikeitimą. Dėl dvimačio objekto, žinomo kaip apskritimas, sukimosi, gaunama trimatė sferos forma.

Sužinokite daugiau,

• Sfera
• Sferos paviršiaus plotas

Sferos tūrio apibrėžimas

Rutulio tūris yra bendra masė, gauta rutulio paviršiaus. Tai 3-D erdvė sferos viduje. Tai priklauso nuo sferos spindulio. Toliau pateiktame paveikslėlyje parodyta r spindulio sfera ir jos tūris.

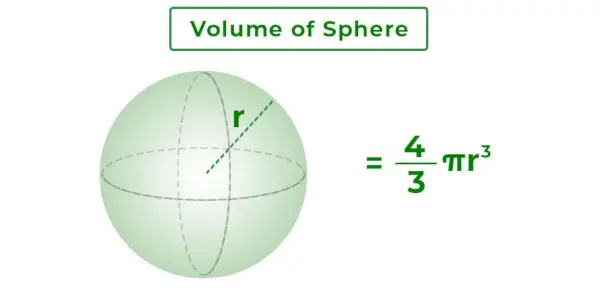
Sferos formulės tūris

Sferos tūrio formulė yra formulė, kuri naudojama norint rasti sferos tūrį, kai nurodomas jos spindulys. R spindulio rutulio formulės tūris pridedamas žemiau,

Sferos formulės tūris = 4/3πr ³

kur,

• r yra sferos spindulys
• Pi yra konstanta ir jos reikšmė yra 22/7

Sfera paprastai skirstoma į dvi kategorijas, kurios yra

• Kietosios sferos tūris
• Tuščiavidurės sferos tūris

Sužinokime apie juos išsamiai.

Kietos sferos tūris

Kieta sfera yra rutulys, kuris yra visiškai užpildytas iki vidaus. y., jo masė iki šerdies ir tūrio formulė, kai spindulys r yra,

Kietosios sferos tūris(V) = (4/3)πr ³

Tuščiavidurės sferos tūris

Tuščiavidurės sferos vidinė erdvė tuščia ir tarkime, kad jos išorinis spindulys yra toks R o jo vidinis spindulys yra r, tada jo tūris apskaičiuojamas pagal formulę,

Tuščiavidurės sferos tūris = (4/3)π(R ³ – r ³ )

Sferos formulės išvedimo tūris

Sferos formulės tūrį galima nustatyti naudojant šiuos metodus:

• Integracijos naudojimas
• Naudojant Archimedo ryšį tarp cilindro, kūgio ir sferos

Išsamiai aptarkime šiuos metodus taip:

Sferos tūris naudojant integraciją

Naudodami integravimo metodą galime tiesiog apskaičiuoti sferos tūrį.

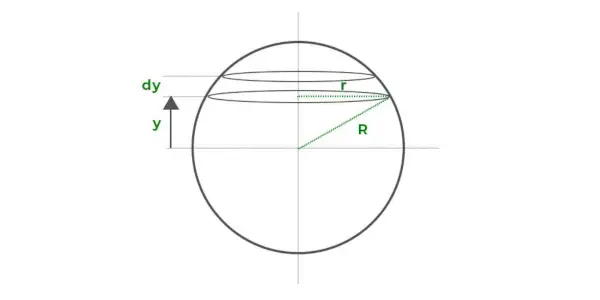
Tarkime, kad sferos tūris sudarytas iš plonų apskritų diskų, sukrautų vienas ant kito, kaip parodyta aukščiau esančioje diagramoje. Kiekvieno plono disko spindulys yra r, o dy storis yra y atstumu nuo x ašies.

Tegul disko tūris yra dV. dV vertė apskaičiuojama taip,

dV = (πr²) tu

Taigi, dV = π (R²- ir²) tu

Bendras sferos tūris bus visų šių mažų diskų tūrių suma. Reikiamą reikšmę galima gauti integravus išraišką nuo ribos -R į R.

Taigi, sferos tūris tampa

V =int_{y=-R}^{y=R} dV

⇒ V =int_{y=-R}^{y=R}π(R^2 – y^2)dy

⇒ V =pi|(R^2y – frac{y^3}{3})dy|_{y=-R}^{y=R}

⇒ V =pi left[R^3-frac{R^3}{3}-(-R^3+frac{R^3}{3}) ight]

⇒ V =pi left[2R^3-frac{2R^3}{3} ight]

⇒ V =frac{4}{3}pi R^3

Taigi gaunama sferos tūrio formulė.

Sferos tūris naudojant Archimedo ryšius

Kaip jau įrodė Archimedas, jei kūgio, rutulio ir cilindro spindulys r ir aukštis yra vienodi, jų tūriai yra 1:2:3.

Todėl galime pasakyti:

Cilindro tūris = kūgio tūris + sferos tūris

Taigi, sferos tūris = cilindro tūris – kūgio tūris

Kaip žinome, tas cilindro tūris = πr²h ir kūgio tūris = (1/3)πr²h

Pakeitę šias reikšmes į lygtį, gauname:

Sferos tūris = πr²h – (1/3)πr²h = (2/3)πr²h

Darome prielaidą, kad cilindro aukštis lygus sferos skersmeniui, kuris yra 2r. Taigi:

Sferos tūris yra (2/3)πr ² h = (2/3)πr ² (2r) = (4/3)πr ³

Taip pat patikrinkite

• Sferinės dangtelio tūrio formulė
• Sferinio sektoriaus formulė
• Sferinio segmento formulė

Kaip apskaičiuoti sferos tūrį?

Sferos tūris yra erdvė, kurią užima rutulys. Jo tūrį galima apskaičiuoti pagal formulę V = 4/3πr ³ .

Norint apskaičiuoti rutulio tūrį, reikia atlikti šiuos veiksmus:

1 žingsnis: Pažymėkite sferos spindulio reikšmę.

rugsėjo 2 d.: Raskite spindulio kubą.

3 veiksmas: Spindulio kubą padauginkite iš (4/3)π

4 veiksmas: Pridėkite (vienetą)³iki galutinio atsakymo.

Pavyzdys sferos tūriui apskaičiuoti

Pavyzdys: Raskite 7 cm spindulio rutulio tūrį.

Pateikta, r = 7 cm

V = (4/3)πr³

Rutulio tūris, V = ((4/3) × π × 7³) cm³

Aukštis = 1436,8 cm³

Taigi sferos tūris yra 1436,8 cm³

Skaityti daugiau

• Kūgio tūris
• Kubo tūris
• Cilindro tūris

Sferos pavyzdžių tūris

1 pavyzdys. Raskite rutulio, kurios spindulys yra 9 cm, tūrį.

Sprendimas:

Turime, r = 9

Rutulio tūris = 4/3 πr³

⇒ Sferos tūris = (4/3) (3,14) (9) (9) (9)

⇒ Sferos tūris = (4) (3.14) (3) (9) (9)

⇒ Sferos tūris = 3052 cm³

2 pavyzdys. Raskite rutulio, kurios spindulys yra 12 cm, tūrį.

Sprendimas:

Turime, r = 12

Rutulio tūris = 4/3 πr³

⇒ Sferos tūris = (4/3) (3,14) (12) (12) (12)

⇒ Sferos tūris = (4) (3.14) (4) (12) (12)

⇒ Sferos tūris = 7234,56 cm³

3 pavyzdys. Raskite sferos, kurios spindulys yra 6 cm, tūrį.

Sprendimas:

Turime, r = 6

Rutulio tūris = 4/3 πr³

⇒ Sferos tūris = (4/3) (3,14) (6) (6) (6)

⇒ Sferos tūris = (4) (3.14) (2) (6) (6)

⇒ Sferos tūris = 904,32 cm³

4 pavyzdys. Raskite rutulio, kurios spindulys yra 4 cm, tūrį.

Sprendimas:

Turime, r = 4

Rutulio tūris = 4/3 πr3

⇒ Sferos tūris = (4/3) (3.14) (4) (4) (4)

⇒ Sferos tūris = (1,33) (3,14) (4) (4) (4)

⇒ Sferos tūris = 267,27 cm³

5 pavyzdys. Raskite 10 cm skersmens rutulio tūrį.

Sprendimas:

Turime 2r = 10

java maišant į int

⇒ r = 5

Sferos tūris = 4/3 πr³

⇒ Sferos tūris = (4/3) (3.14) (5) (5) (5)

⇒ Sferos tūris = (1,33) (3,14) (5) (5) (5)

⇒ Sferos tūris = 522,025 cm³

6 pavyzdys. Raskite 16 cm skersmens rutulio tūrį.

Sprendimas:

Turime 2r = 16

⇒ r = 8

Rutulio tūris = 4/3 πr³

⇒ Sferos tūris = (4/3) (3,14) (8) (8) (8)

⇒ Sferos tūris = (1,33) (3,14) (8) (8) (8)

⇒ Sferos tūris = 2138,21 cm³

7 pavyzdys. Raskite 14 cm skersmens rutulio tūrį.

Sprendimas:

Turime 2r = 14

⇒ r = 7

Rutulio tūris = 4/3 πr³

⇒ Sferos tūris = (4/3) (3,14) (7) (7) (7)

⇒ Sferos tūris = (1,33) (3,14) (7) (7) (7)

⇒ Sferos tūris = 1432,43 cm³

Sferos praktikos klausimų tomas

Q1: Raskite 34 cm skersmens rutulio tūrį.

Q2: Raskite tuščiavidurės sferos, kurios vidinis skersmuo yra 4 cm, o išorinis spindulys 8 cm, tūrį.

3 klausimas: Raskite sferos, kurios spindulys yra 14 cm, tūrį.

4 klausimas: Koks yra rutulio, kurio spindulys lygus kvadrato, kurio plotas 144 m, kraštinei².

Sferos DUK kiekis

Kas yra sferos tūris?

Sferos tūris yra erdvė, kurią užima sferos paviršius.

Koks yra sferos formulės paviršiaus plotas?

Bendras rutulio paviršiaus plotas, kurio spindulys r yra, Plotas = 4πr ²

Kokia yra sferos tūrio formulė?

Rutulio, kurio spindulys r, tūris yra Tūris = 4/3πr ³

Kaip rasti pusrutulio tūrį?

Pusrutulio, kurio spindulys r, tūris yra Tūris = 2/3πr ³

Koks yra sferos ir pusrutulio tūrio santykis?

Jei rutulio ir pusrutulio spindulys yra vienodas, tada jų tūrio santykis yra

IN ₁ : IN ₂ = (4/3πr ³ ): (2/3πr ³ ) = 2:1

Kas yra sferos tūrio vienetas?

Sferos tūris matuojamas m³, cm³, litrai ir kt. m ³ yra standartinis matavimo vienetas.

Koks yra rutulio tūris, kai jo spindulys sumažintas per pusę?

Rutulio tūris = (4/3)πr³= (4/3)π(r/2)³= (4/3)π(r³/8) = Tomas/8. Taigi sferos tūris tampa aštuntadaliu.