Prizmės paviršiaus plotas: Matematikoje prizmė yra esminis daugiakampių šeimos narys ir apibrėžiamas kaip trimatė forma, turinti du identiškus daugiakampius, nukreiptus vienas į kitą ir sujungtus stačiakampiais arba lygiagretainiais paviršiais. Identiški daugiakampiai gali būti trikampiai, kvadratai, stačiakampiai, penkiakampiai arba bet kuris kitas n kraštų daugiakampis ir yra vadinami prizmės pagrindais. Kiti prizmės paviršiai yra lygiagrečiai arba stačiakampiai.

Šiame straipsnyje aptarsime skirtingų tipų prizmės ir prizmės formulės paviršiaus plotas su pavyzdžiais ir praktiniais uždaviniais.

Turinys

• Koks yra prizmės paviršiaus plotas?
• Įvairių tipų prizmės
• Trikampė prizmė
• Stačiakampė prizmė
• Kvadratinė prizmė
• Penkiakampė prizmė
• Šešiakampė prizmė
• Prizmės formulės paviršiaus plotas
• Prizmės paviršiaus plotas Išspręsti pavyzdžiai
• Praktikos problemos dėl prizmės paviršiaus

Koks yra prizmės paviršiaus plotas?

Prizmės paviršiaus plotas vadinamas bendru plotu, kurį sudaro visi jos paviršiai. Norėdami nustatyti prizmės paviršiaus plotą, turime apskaičiuoti kiekvieno jos paviršiaus plotus ir pridėti gautus plotus. Prizmė turi dviejų tipų paviršiaus plotus, būtent šoninį paviršiaus plotą ir bendrą paviršiaus plotą. Plotas, kurį užima prizmės paviršiai, neįskaitant dviejų lygiagrečių paviršių (prizmės pagrindų), vadinamas jos šoniniu paviršiaus plotu.

Prizmės šoninio paviršiaus plotas = [pagrindo perimetras × aukštis] kvadratiniai vienetai

Dabar prizmės bendras paviršiaus plotas yra jos dviejų pagrindų ir šoninio paviršiaus plotų suma.

Bendra bet kokio tipo dešiniosios prizmės bendro paviršiaus ploto apskaičiavimo formulė yra tokia:

Bendras prizmės paviršiaus plotas = [2 (pagrindo plotas) + (pagrindo perimetras × aukštis)] kvadratiniai vienetai

Įvairių tipų prizmės

Pagal prizmės pagrindo formą yra įvairių prizmių tipų, pvz

• trikampės prizmės,
• Kvadratinės prizmės,
• Stačiakampės prizmės,
• Penkiakampės prizmės,
• Šešiakampės prizmės,
• Aštuonkampės prizmės.

Trikampė prizmė

Prizmė su trikampiu pagrindu vadinama trikampe prizme. Trikampė prizmė susideda iš trijų pasvirusių stačiakampių paviršių ir dviejų lygiagrečių trikampių pagrindų. Tegu H yra trikampės prizmės aukštis; a, b ir c yra kraštinių ilgiai, o h yra trikampio pagrindo aukštis.

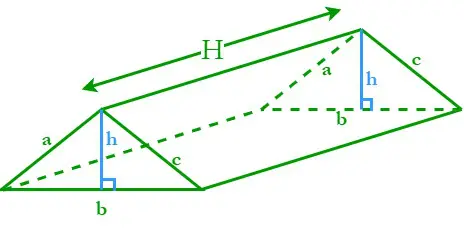
Trikampio pagrindo perimetras (P) = jo trijų kraštinių suma = a + b + c

Trikampio pagrindo plotas (A) = ½ × pagrindas × aukštis = ½ bh

Mes žinome, kad bendroji formulė Dešiniosios prizmės šoninio paviršiaus plotas yra L. S. A. = PH, kur P yra pagrindo perimetras, o A yra pagrindo plotas.

Pakeitę visas reikšmes bendrojoje formulėje gauname ,

Trikampės prizmės šoninio paviršiaus plotas = (a + b +c)H kvadratiniai vienetai

kur,

a, b, c yra trikampio pagrindo kraštinės

H yra trikampės prizmės aukštis

Žinome, kad bendroji dešinės prizmės bendro paviršiaus ploto formulė yra T. S. A. = PH+2A, kur P – pagrindo perimetras, A – pagrindo plotas, o H – prizmės aukštis.

Pakeitę visas reikšmes bendrojoje formulėje gauname

Bendras trikampės prizmės paviršiaus plotas = (a + b + c)H + 2 × (½ bh)

Bendras trikampės prizmės paviršiaus plotas = (a + b + c)H + bh kvadratiniai vienetai

kur,

a, b, c yra trikampio pagrindo kraštinės

H yra trikampės prizmės aukštis

h yra trikampio aukštis

Stačiakampė prizmė

Prizmė su stačiakampiu pagrindu vadinama stačiakampe prizme. Stačiakampė prizmė susideda iš keturių stačiakampių paviršių ir dviejų lygiagrečių stačiakampių pagrindų. Tegul prizmės aukštis yra h, o stačiakampių pagrindų ilgis ir plotis atitinkamai l ir w .

Stačiakampio pagrindo perimetras (P) = keturių jo kraštinių suma = 2 (l + w)

Stačiakampio pagrindo plotas (A) = ilgis × plotis = l × w

python programavimo operatoriai

Žinome, kad bendroji dešinės prizmės šoninio paviršiaus ploto formulė yra L. S. A. = PH, kur P yra pagrindo perimetras, o A yra pagrindo plotas.

Pakeitę visas reikšmes bendrojoje formulėje gauname ,

Stačiakampės prizmės šoninio paviršiaus plotas = 2h(l + w) kvadratiniai vienetai

kur,

l yra ilgis

w yra plotis

h yra aukštis

Žinome, kad bendroji stačios prizmės bendro paviršiaus ploto formulė yra T. S. A. = PH+2A, kur P – pagrindo perimetras, A – pagrindo plotas, o H – prizmės aukštis.

Pakeitę visas reikšmes bendrojoje formulėje gauname

Bendras stačiakampės prizmės paviršiaus plotas = 2h(l + w) + 2(l × w)

= 2 lh + 2 wh + 2 lw

Bendras stačiakampės prizmės paviršiaus plotas = 2 (lh + wh + lw) kvadratiniai vienetai

kur,

l yra ilgis

w yra plotis

h yra aukštis

Kvadratinė prizmė

Prizmė su kvadratiniu pagrindu vadinama kvadratine prizme. Kvadratinė prizmė susideda iš keturių stačiakampių paviršių ir dviejų lygiagrečių kvadratinių pagrindų. Tegul prizmės aukštis yra h, o kvadratinių pagrindų ilgis yra s.

Kvadratinės bazės perimetras (P) = jo keturių kraštinių suma = s + s + s + s = 4s

Kvadratinės bazės plotas (A) = (kraštinės ilgis)²= s²

Žinome, kad bendroji dešinės prizmės šoninio paviršiaus ploto formulė yra L. S. A. = PH, kur P yra pagrindo perimetras, o A yra pagrindo plotas.

Pakeitę visas reikšmes bendrojoje formulėje, gauname,

Kvadratinės prizmės šoninio paviršiaus plotas = 4 kvadratiniai vienetai

kur,

s yra kvadratinio pagrindo pusė

h yra kvadratinės prizmės aukštis

Žinome, kad bendroji dešinės prizmės bendro paviršiaus ploto formulė yra T. S. A. = PH+2A, kur P yra pagrindo perimetras, A yra pagrindo plotas, o H yra prizmės aukštis.

Pakeitę visas bendrosios formulės reikšmes, gauname

Bendras kvadratinės prizmės paviršiaus plotas = [4sh + 2s ² ] kvadratinių vienetų

kur,

s yra kvadratinio pagrindo pusė

h yra kvadratinės prizmės aukštis

Penkiakampė prizmė

Prizmė su penkiakampiu pagrindu vadinama penkiakampe prizme. Penkiakampė prizmė susideda iš penkių pasvirusių stačiakampių paviršių ir dviejų lygiagrečių penkiakampių pagrindų. Tegu h yra penkiakampės prizmės aukštis; a ir b yra penkiakampio pagrindo apotemos ilgis ir kraštinių ilgiai.

Penkiakampio pagrindo perimetras (P) = penkių jo kraštinių suma = 5b

Penkiakampio pagrindo plotas (A) = 5/2 x (apotemos ilgis) x (kraštinės ilgis) = 5ab

Žinome, kad bendroji dešinės prizmės šoninio paviršiaus ploto formulė yra L. S. A. = PH, kur P yra pagrindo perimetras, o A yra pagrindo plotas.

Pakeitę visas reikšmes bendrojoje formulėje, gauname,

Penkiakampės prizmės šoninio paviršiaus plotas = 5bh kvadratiniai vienetai

kur,

b yra penkiakampio pagrindo pusė

h yra penkiakampės prizmės aukštis

Žinome, kad bendroji stačios prizmės bendro paviršiaus ploto formulė yra T. S. A. = PH+2A, kur P – pagrindo perimetras, A – pagrindo plotas, o H – prizmės aukštis.

Pakeitę visas reikšmes bendrojoje formulėje, gauname,

Bendras penkiakampės prizmės paviršiaus plotas = [5bh + 5ab] kvadratiniai vienetai

kur,

b yra penkiakampio pagrindo pusė

a yra apotemos ilgis.

h yra penkiakampės prizmės aukštis

Šešiakampė prizmė

Prizmė su šešiakampiu pagrindu vadinama šešiakampe prizme. Šešiakampė prizmė susideda iš šešių pasvirusių stačiakampių paviršių ir dviejų lygiagrečių šešiakampių pagrindų. Tegu h yra šešiakampės prizmės aukštis; a yra šešiakampių pagrindų šoniniai ilgiai.

Šešiakampio pagrindo perimetras (P) = šešių jo kraštinių suma = 6a

charat java

Šešiakampio pagrindo plotas (A) = 6 x (lygiakraščio trikampio plotas)

A = 6 x (√3a²/4) ⇒ A = 3√3a²/2

Žinome, kad bendroji dešinės prizmės šoninio paviršiaus ploto formulė yra L. S. A. = PH, kur P yra pagrindo perimetras, o A yra pagrindo plotas.

Pakeitę visas reikšmes bendrojoje formulėje, gauname,

Šešiakampės prizmės šoninio paviršiaus plotas = 6ah kvadratiniai vienetai

kur,

a yra šešiakampio pagrindo pusė

h yra šešiakampio pagrindo aukštis

Žinome, kad bendroji stačios prizmės bendro paviršiaus ploto formulė yra T. S. A. = PH+2A, kur P – pagrindo perimetras, A – pagrindo plotas, o H – prizmės aukštis.

Pakeitę visas reikšmes bendrojoje formulėje gauname

Bendras šešiakampės prizmės paviršiaus plotas = [6ah +3√3a²] kvadratinių vienetų

kur,

a yra šešiakampio pagrindo pusė

h yra šešiakampio pagrindo aukštis:

Prizmės formulės paviršiaus plotas

Žemiau pateiktoje lentelėje pateikiama skirtingų tipų prizmių formulė:

Prizmės paviršiaus plotas Išspręsti pavyzdžiai

1 uždavinys: Koks yra prizmės, kurios pagrindo plotas yra 36 kvadratiniai vienetai, pagrindo perimetras – 24 vienetai, o bendras paviršiaus plotas – 320 kvadratinių vienetų, aukštis?

Sprendimas:

Pateikti duomenys,

Pagrindo plotas = 36 kvadratiniai vienetai

Pagrindo perimetras = 24 vnt

Bendras prizmės paviršiaus plotas = 320 kvadratinių vienetų

Mes turime,

Bendras prizmės paviršiaus plotas = (2 × pagrindo plotas) + (pagrindo perimetras × aukštis)

⇒ 320 = (2 × 36) + (24 × h)

⇒ 24h = 248 ⇒ h = 10,34 vnt

Vadinasi, duotosios prizmės aukštis yra 10,34 vienetų.

2 uždavinys: Raskite bendrą kvadratinės prizmės paviršiaus plotą, jei prizmės aukštis ir kvadratinio pagrindo kraštinės ilgis yra atitinkamai 13 cm ir 4 cm.

Sprendimas:

Pateikti duomenys,

Kvadratinės prizmės aukštis (h) = 13 cm

Kvadratinio pagrindo kraštinės ilgis (a) = 4 cm

Mes tai žinome,

Bendras kvadratinės prizmės paviršiaus plotas = 2a²+ 4h

= 2 × (4)²+ 4 × 4 × 13

= 32 + 208 = 240 cm²

Vadinasi, bendras duotosios prizmės paviršiaus plotas yra 240 kv.cm.

3 uždavinys: nustatykite penkiakampės prizmės pagrindo ilgį, jei jos bendras plotas yra 100 kvadratinių vienetų, o aukštis ir apotemos ilgis yra atitinkamai 8 vienetai ir 5 vienetai.

Sprendimas:

Pateikti duomenys,

Bendras penkiakampės prizmės paviršiaus plotas = 100 kvadratinių vienetų

Prizmės aukštis (h) = 8 vnt

Apotemos ilgis (a) = 5 vnt

Mes tai žinome,

Bendras penkiakampės prizmės paviršiaus plotas = 5ab + 5bh

⇒ 100 = 5b (a+ h)

⇒ 100/5 = b (5 + 8)

⇒ 20 = b × (13) ⇒ b = 25/16 = 1,54 vnt.

Vadinasi, pagrindo ilgis yra 1,54 vnt

4 problema: Nustatykite stačiakampės prizmės aukštį ir bendrą stačiakampės prizmės plotą, jei jos šoninio paviršiaus plotas yra 540 kv. cm, o pagrindo ilgis ir plotis yra atitinkamai 13 cm ir 7 cm.

Sprendimas:

Pateikti duomenys,

Stačiakampio pagrindo ilgis (l) = 13 cm

Stačiakampio pagrindo plotis (w) = 7 cm

Prizmės šoninio paviršiaus plotas = 540 kv.cm

Mes turime,

Prizmės šoninio paviršiaus plotas = pagrindo perimetras × aukštis

⇒ 540 = 2 (l + w) h

⇒ 2 (13 + 7) h = 540

⇒ 2 (20) h = 540 ⇒ h = 13,5 cm

1 eilės logika

Mes tai žinome,

Bendras stačiakampės prizmės paviršiaus plotas = 2 (lw + wh + lh)

= 2 × (13 × 7 + 7 × (13,5) + 13 × (13,5))

= 2 × (91 + 94,5 + 175,5) = 722 kv. cm

Vadinasi, duotosios stačiakampės prizmės aukštis ir bendras paviršiaus plotas yra atitinkamai 13,5 cm ir 722 kv. cm.

5 uždavinys: nustatykite taisyklingosios šešiakampės prizmės paviršiaus plotą, jei prizmės aukštis yra 12 colių, o pagrindo kraštinės ilgis yra 5 coliai.

Sprendimas:

Pateikti duomenys,

Prizmės aukštis (h) = 12 colių

Pagrindo kraštinės ilgis (a) = 6 coliai

Taisyklingos šešiakampės prizmės paviršiaus plotas = 6ah + 3√3a²

= 6 × 5 × 12 + 3√3 (5)²

= 360 + 75√3

= 360 + 75 × (1,732) = 489,9 kv. colio

Vadinasi, duotosios prizmės paviršiaus plotas yra 489,9 kv.

6 uždavinys: Apskaičiuokite trikampės prizmės, kurios pagrindo perimetras yra 25 coliai, trikampio pagrindo ilgis ir aukštis yra 9 coliai ir 10 colių, o prizmės aukštis yra 14 colių, šoninio ir bendro paviršiaus plotus.

Sprendimas:

Pateikti duomenys,

Prizmės aukštis (H) = 14 colių

Pagrindinis prizmės perimetras (P) = 25 coliai

Trikampio pagrindo ilgis = 9 coliai

Trikampio aukštis = 10 colių

Mes tai žinome,

Prizmės šoninio paviršiaus plotas = pagrindo perimetras × aukštis

= 25 × 14 = 350 kv. colių

Trikampio pagrindo plotas (A) = ½ × pagrindas × aukštis = 1/2 × 9 × 10 = 45 kv.

Bendras trikampės prizmės paviršiaus plotas = 2A + PH

= 2 × 45 + 25 × 14 = 90 + 350 = 440 kv. colių

Vadinasi, prizmės šoninis ir bendras paviršiaus plotai yra atitinkamai 350 kv. colių ir 440 kv. colių.

java ciklas

Praktikos problemos dėl prizmės paviršiaus

1. Duota stačiakampė prizmė, kurios matmenys:

• Ilgis = 6 cm
• Plotis = 4 cm
• Aukštis = 5 cm

Apskaičiuokite bendrą paviršiaus plotą.

2. Apsvarstykite trikampę prizmę, kurios matmenys:

• Trikampio pagrindas = 8 cm
• Trikampio aukštis = 6 cm
• Prizmės ilgis = 10 cm

Raskite bendrą paviršiaus plotą.

3. Nustatykite taisyklingos penkiakampės prizmės paviršiaus plotą:

• Pagrindo kraštinės ilgis = 7 cm
• Prizmės aukštis = 9 cm.

4. Apskaičiuokite šešiakampės prizmės paviršiaus plotą:

• Įprasto šešiakampio pagrindo kraštinės ilgis = 10 cm
• Prizmės aukštis = 12 cm.

Prizmės paviršiaus plotas – DUK

Kas yra prizmė geometrijoje?

Prizmė yra trimatė forma, turinti du lygiagrečius pagrindus ir juos jungiančius stačiakampius arba lygiagretainius šoninius paviršius. Prizmės būna įvairių formų, pavyzdžiui, stačiakampės prizmės, trikampės prizmės ir penkiakampės prizmės, kurių kiekviena turi unikalių savybių.

Kaip rasti prizmės paviršiaus plotą?

Norėdami rasti prizmės paviršiaus plotą, apskaičiuokite visų jos paviršių plotus ir susukite juos. Stačiakampės prizmės paviršiaus ploto formulė yra 2lw + 2lh + 2wh, kur l yra ilgis, w yra plotis ir h yra aukštis. Kitų tipų prizmėms, pavyzdžiui, trikampėms arba penkiakampėms prizmėms, gali prireikti papildomų bazinio ploto ir šoninio ploto formulių.

Kokios yra prizmės savybės?

Prizmės turi keletą pagrindinių savybių:

• Jie turi dvi lygiagrečias bazes.
• Visi šoniniai paviršiai yra lygiagretainiai.
• Aukštis (aukštis) yra statmenas atstumas tarp dviejų bazių.
• Pagrindai yra vienodi pagal formą ir dydį.
• Skerspjūvis lygiagretus pagrindams visada yra tokios pat formos ir dydžio kaip ir pagrindai.

Kokie yra realaus gyvenimo prizmių pavyzdžiai?

Prizmų galima rasti įvairiuose kasdieniuose daiktuose ir konstrukcijose. Pavyzdžiai:

• Stačiakampės prizmės: pastatai, javų dėžės, knygos.
• Trikampės prizmės: Namų stogai, pleišto formos objektai.
• Penkiakampės prizmės: kai kurių tipų kolonos, tam tikros architektūrinės konstrukcijos.
• Šešiakampės prizmės: tam tikrų tipų kristalai, kai kurie pakavimo konteineriai.

Kodėl prizmėse svarbus paviršiaus plotas?

Paviršiaus plotas yra labai svarbus prizmėse, nes jis reiškia bendrą visų prizmės paviršių (veidų) plotą. Paviršiaus ploto supratimas padeda įvairiose praktinėse srityse, pavyzdžiui, apskaičiuojant medžiagos kiekį, reikalingą prizmės formos objektui pastatyti ar uždengti, nustatyti šilumos perdavimo greitį ir optimizuoti pakuotės dizainą.