Rekursinė funkcija gali būti apibrėžta kaip rutina, kuri iškviečia save tiesiogiai arba netiesiogiai.

Kitaip tariant, rekursinė funkcija yra funkcija, kuri išsprendžia problemą sprendžiant mažesnius tos pačios problemos atvejus. Ši technika dažniausiai naudojama programuojant sprendžiant problemas, kurias galima suskirstyti į paprastesnes, panašias subproblemas.

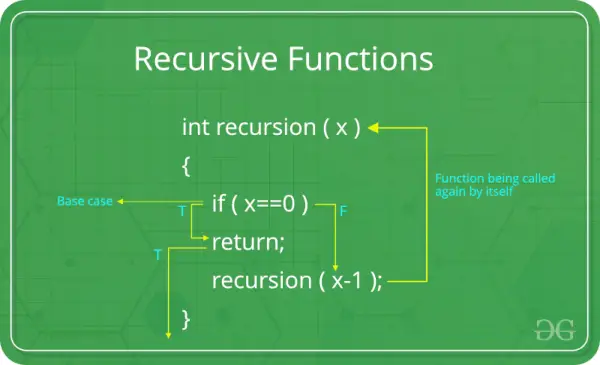
Rekursinės funkcijos poreikis:

Rekursyvinė funkcija yra funkcija, kuri išsprendžia problemą sprendžiant mažesnius tos pačios problemos atvejus. Ši technika dažnai naudojama programuojant sprendžiant problemas, kurias galima suskirstyti į paprastesnes, panašias subproblemas.

1. Sudėtingų užduočių sprendimas:

Rekursinės funkcijos suskaido sudėtingas problemas į mažesnius tos pačios problemos atvejus, todėl gaunamas kompaktiškas ir skaitomas kodas.

2. Skaldyk ir valdyk:

Rekursyvinės funkcijos yra tinkamos dalyti ir užkariauti algoritmams, tokiems kaip rūšiavimo ir greito rūšiavimo sujungimas, problemų suskaidymas į smulkesnes dalis, rekursyvus sprendimas ir sprendimų sujungimas su pradine problema.

režisierius Karanas Joharas

3. Atsitraukimas :

Rekursyvus atgalinis sekimas idealiai tinka tyrinėjant ir sprendžiant tokias problemas kaip N-Queens ir Sudoku.

4. Dinaminis programavimas:

Rekursinės funkcijos efektyviai išsprendžia dinamines programavimo problemas, spręsdamos subproblemas ir sujungdamos jų sprendimus į pilną sprendimą.

5. Medis ir grafikų struktūros:

Rekursinės funkcijos puikiai tinka dirbant su medžio ir grafiko struktūromis, supaprastinant važiavimo ir modelio atpažinimo užduotis .

Kaip parašyti rekursinę funkciją:

Rekursinės funkcijos komponentai:

Bazinis atvejis: Kiekviena rekursinė funkcija turi turėti pagrindinę raidę. Bazinis atvejis yra paprasčiausias scenarijus, kuriam nereikia tolesnės pasikartojimo. Tai nutraukimo sąlyga, neleidžianti funkcijai išsikviesti savęs neribotą laiką. Be tinkamo bazinio atvejo rekursinė funkcija gali sukelti begalinę rekursiją.

Rekursyvus atvejis: Rekursyviniu atveju funkcija išsikviečia save su pakeistais argumentais. Tai yra rekursijos esmė – didesnės problemos sprendimas suskaidant ją į mažesnius tos pačios problemos atvejus. Rekursyvusis atvejis turėtų priartėti prie bazinio atvejo su kiekviena iteracija.

Panagrinėkime pavyzdį skaičiaus faktorialas :

Šiame pavyzdyje bazinis atvejis yra kai n yra 0 , ir funkcija grąžinama 1 . Rekursyvus atvejis dauginasi n su parametru iškviestos funkcijos rezultatu n – 1 . Procesas tęsiamas tol, kol pasiekiamas pagrindinis atvejis.

Labai svarbu užtikrinti, kad rekursinė funkcija turėtų teisingą bazinį dydį ir kad rekursiniai iškvietimai nukreiptų į bazinį dydį, kitaip procedūra gali būti vykdoma neribotą laiką, o tai gali sukelti krūvos perpildymą (viršijant laisvą atmintį, skirtą funkcijų iškvietimams).

Žemiau pateikiamas skaičiaus faktorialo įgyvendinimas:

#include  using namespace std; // Recursive Function to calculate Factorial of a number int factorial(int n) {  // Base case  if (n == 0) {  return 1;  }  // Recursive case  return n * factorial(n - 1); } // Driver Code int main() {  int n = 4;  cout << 'Factorial of ' << n  << ' is:' << factorial(n);  return 0; }>

import java.util.Scanner; public class Factorial {  // Recursive Function to calculate the factorial of a number  static int factorial(int n) {  // Base case: If n is 0, the factorial is 1.  if (n == 0) {  return 1;  }  // Recursive case: Calculate the factorial by multiplying n with the factorial of (n - 1).  return n * factorial(n - 1);  }  public static void main(String[] args) {  int n = 4;  // Calculate and print the factorial of n.  int result = factorial(n);  System.out.println('Factorial of ' + n + ' is: ' + result);  } }>

# Recursive Function to calculate Factorial of a number def factorial(n): # Base case if n == 0: return 1 # Recursive case return n * factorial(n - 1) # Driver Code if __name__ == '__main__': n = 4 print('Factorial of', n, 'is:', factorial(n))>

using System; class Program {  // Recursive Function to calculate Factorial of a number  static int Factorial(int n)  {  // Base case  if (n == 0)  {  return 1;  }  // Recursive case  return n * Factorial(n - 1);  }  // Driver Code  static void Main()  {  int n = 4;  Console.WriteLine('Factorial of ' + n + ' is: ' + Factorial(n));  } }>

// Function to calculate the factorial of a number using recursion function factorial(n) {  // Base case: If n is 0, the factorial is 1.  if (n === 0) {  return 1;  }  // Recursive case: Calculate the factorial by multiplying n with the factorial of (n - 1).  return n * factorial(n - 1); } // Main function function main() {  // Given number  let n = 4;  // Calculate the factorial of n.  let result = factorial(n);  // Print the result  console.log('Factorial of ' + n + ' is: ' + result); } // Call the main function main();>

Factorial of 4 is:24>

Laiko sudėtingumas: O(n)
Pagalbinė erdvė: O(n)