Normalioji jėga apibrėžiama kaip jėga, kurią bet koks paviršius veikia kitą objektą. Kai objektas yra ramybės būsenoje, jį veikianti grynoji jėga yra lygi nuliui. Įprasta jėga negali būti taikoma dviem paviršiams, kurie nėra sujungti vienas su kitu. Jis gali būti interpretuojamas kaip jėgos komponentas, kuris yra vertikalus bet kuriam kontaktiniam paviršiui. Jis nustato, kokią jėgą kūnas perduoda žemei. Normalioji jėga yra lygi objekto svoriui tik tuo atveju, jei objekto greičio kitimo greitis yra neigiamas, o tai reiškia, kad jis lėtėja.

Formulė

Normalios jėgos vertė priklauso nuo to, kur objektas yra kito objekto atžvilgiu. Kai objektas ketina kristi, padėtis, kurioje objektas krenta ant žemės, lemia normalios jėgos vertę. Normali jėga žymima simboliu F_N. Jo matavimo vienetas yra niutonai (N), o matmenų formulė pateikiama [M¹L¹T^-2].

Jei kūnas remiasi plokščia jėga, normalioji jėga yra lygi gravitacinio svorio dydžiui, ty mg.

F _N = mg

kur,

F_Nyra normali jėga,

m yra ramybės objekto masė,

g – pagreitis dėl gravitacijos.

Jei kūnas tam tikru kampu slysta žemyn nuo nuožulnaus paviršiaus, normaliosios jėgos reikšmė yra gravitacinis svoris, pridėtas prie papildomos jėgos F sin θ. Šiuo atveju normalioji jėga yra didesnė už objekto svorį.

F _N = mg + F sin θ

kur,

F_Nyra normali jėga,

m yra slenkančio objekto masė,

g yra pagreitis dėl gravitacijos,

θ yra polinkio kampas.

Jei jėga veikia kūną aukštyn, normaliosios jėgos vertė yra gravitacinis svoris, sumažintas jėga F sin θ. Šiuo atveju grynoji normalioji jėga yra mažesnė už objekto svorį.

F _N = mg – F sin θ

kur,

c kodas abs

F_Nyra normali jėga,

m yra slenkančio objekto masė,

g yra pagreitis dėl gravitacijos,

θ yra polinkio kampas.

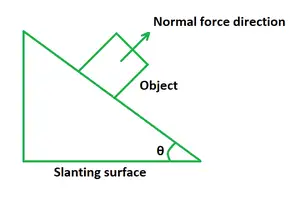
Jei kūnas pastatytas ant nuožulnios plokštumos, normalioji jėga F_Nlygus gravitacinio svorio ir polinkio kampo kosinuso sandaugai.

F _N = mg cos θ

kur,

F_Nyra normali jėga,

m yra slenkančio objekto masė,

g yra pagreitis dėl gravitacijos,

θ yra polinkio kampas.

Pavyzdinės problemos

1 uždavinys. 2 kg masės objektas guli ant stalo. Apskaičiuokite jį veikiančią normalią jėgą.

Sprendimas:

Mes turime,

m = 2

g = 9,8

Naudojant formulę, kurią gauname,

F_N= mg

= 2 (9,8)

= 19,6 N

2 uždavinys. Objektas remiasi į stalą 39,2 N jėga. Apskaičiuokite jį veikiančią normaliąją jėgą.

Sprendimas:

Mes turime,

F = 39,2

g = 9,8

Naudojant formulę, kurią gauname,

F_N= mg

=> m = F/g

=> m = 39,2/9,8

=> m = 4 kg

3 uždavinys. 10 kg masės objektas 200 N jėga slysta žemyn nuo nuožulnaus paviršiaus 30° kampu. Apskaičiuokite įprastą jėgą, kuri jį veikia.

... Java

Sprendimas:

Mes turime,

F = 200

m = 10

g = 9,8

θ = 30°

Naudojant formulę, kurią gauname,

F_N= mg + F sin θ

= 10 (9,8) + 200 sin 30°

= 98 + 200 (1/2)

= 98 + 100

= 198 N

4 uždavinys. 20 kg masės objektas 400 N jėga slysta žemyn nuo nuožulnaus paviršiaus 30° kampu. Apskaičiuokite įprastą jėgą, kuri jį veikia.

Sprendimas:

Mes turime,

F = 400

m = 20

g = 9,8

θ = 30°

Naudojant formulę, kurią gauname,

F_N= mg + F sin θ

= 20 (9,8) + 400 sin 30°

= 196 + 400 (1/2)

= 196 + 200

= 396 N

5 uždavinys. 15 kg masės objektas padėtas ant nuožulnaus paviršiaus 30° kampu. Apskaičiuokite įprastą jėgą, veikiančią jį, jei jėga veikia į viršų ir yra 100 N.

Sprendimas:

Mes turime,

F = 100

m = 15

g = 9,8

θ = 30°

Naudojant formulę, kurią gauname,

F_N= mg – F sin θ

= 15 (9,8) – 100 be 30°

= 147–100 (1/2)

= 147–50

= 97 N

6 uždavinys. 5 kg masės objektas padėtas ant nuožulnaus paviršiaus 60° kampu. Apskaičiuokite normalią jėgą, kuri jį veikia bet kuriame taške.

Sprendimas:

simbolis į int java

Mes turime,

m = 5

g = 9,8

θ = 60°

Naudojant formulę, kurią gauname,

F_N= mg cos θ

= 5 (9,8) (cos 60°)

= 49/2

= 24,5 N

7 uždavinys. Daiktas dedamas ant nuožulnaus paviršiaus 60° kampu. Apskaičiuokite jo masę, jei normalioji jėga, kuri ją veikia, yra 400 N.

Sprendimas:

Mes turime,

F_N= 400,

θ = 60°

Naudojant formulę, kurią gauname,

F_N= mg cos θ

m = F/(g cos θ)

= 400/ (9,8 × cos 60°)

= 400/4,9

= 81,63 N