logo

TechCodeview

ML | Lūkesčių maksimizavimo algoritmas

Realiame pasaulyje mašininis mokymasis programas, įprasta turėti daug svarbių funkcijų, tačiau galima pastebėti tik dalį jų. Nagrinėjant kintamuosius, kurie kartais yra stebimi, o kartais ne, iš tiesų galima panaudoti atvejus, kai tas kintamasis yra matomas arba stebimas, siekiant išmokti ir numatyti atvejus, kai jis nėra stebimas. Šis metodas dažnai vadinamas trūkstamų duomenų tvarkymu. Naudodami turimus atvejus, kai kintamasis yra stebimas, mašininio mokymosi algoritmai gali išmokti modelius ir ryšius iš stebimų duomenų. Tada šie išmokti modeliai gali būti naudojami numatant kintamojo reikšmes tais atvejais, kai jo trūksta arba jie nėra pastebimi.

Lūkesčių maksimizavimo algoritmas gali būti naudojamas sprendžiant situacijas, kai kintamieji yra iš dalies stebimi. Kai tam tikri kintamieji yra stebimi, galime naudoti tuos atvejus, kad sužinotume ir įvertintume jų reikšmes. Tada galime numatyti šių kintamųjų reikšmes tais atvejais, kai tai nėra pastebima.

EM algoritmas buvo pasiūlytas ir pavadintas pagrindiniame straipsnyje, kurį 1977 m. paskelbė Arthuras Dempsteris, Nan Lairdas ir Donaldas Rubinas. Jų darbas formalizavo algoritmą ir parodė jo naudingumą statistiniam modeliavimui ir vertinimui.



EM algoritmas taikomas latentiniams kintamiesiems, kurie yra kintamieji, kurie nėra tiesiogiai stebimi, bet yra išvedami iš kitų stebimų kintamųjų reikšmių. Naudodamas žinomą bendrąją tikimybių pasiskirstymo formą, reglamentuojančią šiuos latentinius kintamuosius, EM algoritmas gali numatyti jų reikšmes.
EM algoritmas yra daugelio neprižiūrimų klasterizacijos algoritmų mašininio mokymosi srityje pagrindas. Tai suteikia pagrindą, leidžiantį rasti statistinio modelio vietinius didžiausios tikimybės parametrus ir nustatyti latentinius kintamuosius tais atvejais, kai trūksta duomenų arba jie yra neišsamūs.

Lūkesčių maksimizavimo (EM) algoritmas

Lūkesčių maksimizavimo (EM) algoritmas yra kartotinis optimizavimo metodas, sujungiantis skirtingus neprižiūrimus mašininis mokymasis algoritmai, skirti rasti didžiausią tikimybę arba maksimalius užpakalinius parametrų įverčius statistiniuose modeliuose, kuriuose dalyvauja nepastebimi latentiniai kintamieji. EM algoritmas dažniausiai naudojamas latentiniams kintamųjų modeliams ir gali tvarkyti trūkstamus duomenis. Jį sudaro įvertinimo žingsnis (E-žingsnis) ir maksimizavimo žingsnis (M-žingsnis), sudarantis kartotinį procesą, siekiant pagerinti modelio tinkamumą.

  • E veiksme algoritmas apskaičiuoja latentinius kintamuosius, t. y. log-tikimybės lūkesčius, naudodamas dabartinius parametrų įvertinimus.
  • M žingsnyje algoritmas nustato parametrus, kurie maksimaliai padidina tikėtiną log tikimybę, gautą E žingsnyje, o atitinkami modelio parametrai atnaujinami pagal įvertintus latentinius kintamuosius.
Lūkesčių maksimizavimas EM algoritme-Geeksforgeeks

Lūkesčių maksimizavimas EM algoritme

Iteratyviai kartojant šiuos veiksmus, EM algoritmas siekia maksimaliai padidinti stebimų duomenų tikimybę. Jis dažniausiai naudojamas neprižiūrintoms mokymosi užduotims, tokioms kaip klasterizavimas, kai išvedami latentiniai kintamieji ir yra pritaikyti įvairiose srityse, įskaitant mašininį mokymąsi, kompiuterinį regėjimą ir natūralios kalbos apdorojimą.

Pagrindiniai lūkesčių maksimizavimo (EM) algoritmo terminai

Kai kurie dažniausiai naudojami pagrindiniai lūkesčių maksimizavimo (EM) algoritmo terminai yra šie:

    Latentiniai kintamieji: latentiniai kintamieji yra nepastebimi statistinių modelių kintamieji, kuriuos galima daryti tik netiesiogiai pagal jų poveikį stebimiems kintamiesiems. Jų negalima išmatuoti tiesiogiai, bet galima nustatyti pagal jų poveikį stebimiems kintamiesiems. Tikimybė: tai tikimybė, kad bus stebimi pateikti duomenys, atsižvelgiant į modelio parametrus. EM algoritmo tikslas yra rasti parametrus, kurie padidina tikimybę. Log-Lielihood: Tai tikimybės funkcijos logaritmas, kuris matuoja stebimų duomenų ir modelio suderinamumą. EM algoritmas siekia maksimaliai padidinti log tikimybę. Didžiausios tikimybės įvertinimas (MLE) : MLE yra statistinio modelio parametrų įvertinimo metodas, ieškant parametrų reikšmių, kurios maksimaliai padidina tikimybės funkciją, kuri matuoja, kaip gerai modelis paaiškina stebimus duomenis. Užpakalinė tikimybė: Bajeso išvados kontekste EM algoritmas gali būti išplėstas, kad būtų galima įvertinti maksimalius a posteriori (MAP) įverčius, kai parametrų užpakalinė tikimybė apskaičiuojama remiantis išankstiniu pasiskirstymu ir tikimybės funkcija. Laukimo (E) žingsnis: EM algoritmo E žingsnis apskaičiuoja latentinių kintamųjų numatomą vertę arba užpakalinę tikimybę, atsižvelgiant į stebimus duomenis ir esamus parametrų įvertinimus. Tai apima kiekvieno latentinio kintamojo tikimybių apskaičiavimą kiekvienam duomenų taškui. Maksimizavimo (M) žingsnis: EM algoritmo M žingsnis atnaujina parametrų įverčius, padidindamas tikėtiną log tikimybę, gautą iš E žingsnio. Tai apima parametrų reikšmių, optimizuojančių tikimybės funkciją, radimą, paprastai naudojant skaitmeninio optimizavimo metodus. Konvergencija: konvergencija reiškia būklę, kai EM algoritmas pasiekė stabilų sprendimą. Paprastai jis nustatomas tikrinant, ar logaritminės tikimybės arba parametrų įvertinimų pokytis nesiekia iš anksto nustatytos ribos.

Kaip veikia lūkesčių maksimizavimo (EM) algoritmas:

Lūkesčių maksimizavimo algoritmo esmė yra naudoti turimus stebimus duomenų rinkinio duomenis trūkstamiems duomenims įvertinti ir naudoti tuos duomenis parametrų reikšmėms atnaujinti. Leiskite mums išsamiai suprasti EM algoritmą.

EM algoritmo srauto diagrama-Geeksforgeeks

EM algoritmo schema

    Inicijavimas:
    • Iš pradžių atsižvelgiama į pradinių parametrų reikšmių rinkinį. Neišsamių stebimų duomenų rinkinys pateikiamas sistemai su prielaida, kad stebimi duomenys gaunami iš konkretaus modelio.
    E-žingsnis (laukimo žingsnis): Šiame žingsnyje mes naudojame stebimus duomenis, kad įvertintume arba atspėtų trūkstamų arba neišsamių duomenų reikšmes. Iš esmės jis naudojamas kintamiesiems atnaujinti.
    • Apskaičiuokite kiekvieno latentinio kintamojo užpakalinę tikimybę arba atsakomybę, atsižvelgiant į stebimus duomenis ir esamus parametrų įvertinimus.
    • Įvertinkite trūkstamas arba neišsamias duomenų reikšmes naudodami dabartinius parametrų įvertinimus.
    • Apskaičiuokite stebimų duomenų loginę tikimybę, remdamiesi dabartiniais parametrų įverčiais ir apskaičiuotais trūkstamais duomenimis.
    M-žingsnis (maksimalizavimo žingsnis): Šiame žingsnyje mes naudojame visus duomenis, sugeneruotus ankstesniame Expectation – žingsnyje, kad atnaujintume parametrų reikšmes. Iš esmės jis naudojamas hipotezei atnaujinti.
    • Atnaujinkite modelio parametrus, maksimaliai padidindami tikėtiną visiško duomenų žurnalo tikimybę, gautą iš E žingsnio.
    • Paprastai tai apima optimizavimo problemų sprendimą, siekiant rasti parametrų reikšmes, kurios padidina žurnalo tikimybę.
    • Naudojama konkreti optimizavimo technika priklauso nuo problemos pobūdžio ir naudojamo modelio.
    Konvergencija: šiame žingsnyje patikrinama, ar reikšmės konverguoja, ar ne, jei taip, sustabdykite, kitaip pakartokite 2 žingsnis ir 3 žingsnis y., Expectation – žingsnis ir Maksimizavimas – žingsnis, kol įvyks konvergencija.
    • Patikrinkite konvergenciją, palygindami log-tikimybės pokytį arba parametrų reikšmes tarp iteracijų.
    • Jei pakeitimas yra mažesnis už iš anksto nustatytą slenkstį, sustokite ir apsvarstykite, kad algoritmas konverguojamas.
    • Kitu atveju grįžkite į E žingsnį ir kartokite procesą, kol pasieksite konvergenciją.

Lūkesčių maksimizavimo algoritmas Žingsnis po žingsnio įgyvendinimas

Importuokite reikiamas bibliotekas

Python3




mycricketlive

import> numpy as np> import> matplotlib.pyplot as plt> from> scipy.stats>import> norm> 

>

>

Sukurkite duomenų rinkinį su dviem Gauso komponentais

Python3




# Generate a dataset with two Gaussian components> mu1, sigma1>=> 2>,>1> mu2, sigma2>=> ->1>,>0.8> X1>=> np.random.normal(mu1, sigma1, size>=>200>)> X2>=> np.random.normal(mu2, sigma2, size>=>600>)> X>=> np.concatenate([X1, X2])> # Plot the density estimation using seaborn> sns.kdeplot(X)> plt.xlabel(>'X'>)> plt.ylabel(>'Density'>)> plt.title(>'Density Estimation of X'>)> plt.show()>

režisierius Karanas Joharas 

>

>

Išvestis :

Tankio sklypas-Geeksforgeeks

Tankio sklypas

Inicijuoti parametrus

Python3




# Initialize parameters> mu1_hat, sigma1_hat>=> np.mean(X1), np.std(X1)> mu2_hat, sigma2_hat>=> np.mean(X2), np.std(X2)> pi1_hat, pi2_hat>=> len>(X1)>/> len>(X),>len>(X2)>/> len>(X)> 

>

>

Atlikite EM algoritmą

  • Pakartojama nurodytam epochų skaičiui (šiuo atveju 20).
  • Kiekvienoje epochoje E-žingsnis apskaičiuoja atsakomybę (gama reikšmes), įvertindamas kiekvieno komponento Gauso tikimybių tankius ir pasverdamas juos atitinkamomis proporcijomis.
  • M veiksmas atnaujina parametrus, apskaičiuodamas kiekvieno komponento svertinį vidurkį ir standartinį nuokrypį

Python3




# Perform EM algorithm for 20 epochs> num_epochs>=> 20> log_likelihoods>=> []> for> epoch>in> range>(num_epochs):> ># E-step: Compute responsibilities> >gamma1>=> pi1_hat>*> norm.pdf(X, mu1_hat, sigma1_hat)> >gamma2>=> pi2_hat>*> norm.pdf(X, mu2_hat, sigma2_hat)> >total>=> gamma1>+> gamma2> >gamma1>/>=> total> >gamma2>/>=> total> > ># M-step: Update parameters> >mu1_hat>=> np.>sum>(gamma1>*> X)>/> np.>sum>(gamma1)> >mu2_hat>=> np.>sum>(gamma2>*> X)>/> np.>sum>(gamma2)> >sigma1_hat>=> np.sqrt(np.>sum>(gamma1>*> (X>-> mu1_hat)>*>*>2>)>/> np.>sum>(gamma1))> >sigma2_hat>=> np.sqrt(np.>sum>(gamma2>*> (X>-> mu2_hat)>*>*>2>)>/> np.>sum>(gamma2))> >pi1_hat>=> np.mean(gamma1)> >pi2_hat>=> np.mean(gamma2)> > ># Compute log-likelihood> >log_likelihood>=> np.>sum>(np.log(pi1_hat>*> norm.pdf(X, mu1_hat, sigma1_hat)> >+> pi2_hat>*> norm.pdf(X, mu2_hat, sigma2_hat)))> >log_likelihoods.append(log_likelihood)> # Plot log-likelihood values over epochs> plt.plot(>range>(>1>, num_epochs>+>1>), log_likelihoods)> plt.xlabel(>'Epoch'>)> plt.ylabel(>'Log-Likelihood'>)> plt.title(>'Log-Likelihood vs. Epoch'>)> plt.show()> 

>

dvejetainės paieškos algoritmas 
>

Išvestis :

Epocha vs Log-likelihood-Geeksforgeeks

Epocha prieš žurnalo tikimybę

Nubraižykite galutinį apskaičiuotą tankį

Python3




# Plot the final estimated density> X_sorted>=> np.sort(X)> density_estimation>=> pi1_hat>*>norm.pdf(X_sorted,> >mu1_hat,> >sigma1_hat)>+> pi2_hat>*> norm.pdf(X_sorted,> >mu2_hat,> >sigma2_hat)> plt.plot(X_sorted, gaussian_kde(X_sorted)(X_sorted), color>=>'green'>, linewidth>=>2>)> plt.plot(X_sorted, density_estimation, color>=>'red'>, linewidth>=>2>)> plt.xlabel(>'X'>)> plt.ylabel(>'Density'>)> plt.title(>'Density Estimation of X'>)> plt.legend([>'Kernel Density Estimation'>,>'Mixture Density'>])> plt.show()> 

>

>

Išvestis :

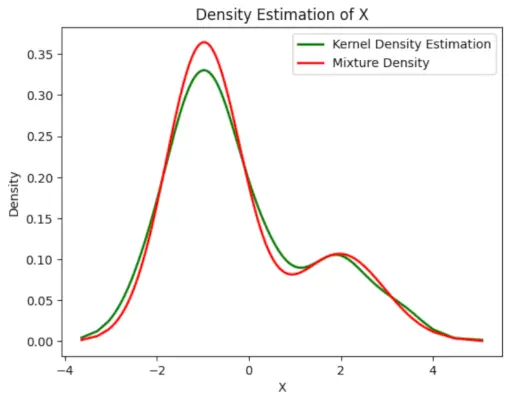
Numatomas tankis-Geeksforgeeks

Numatomas tankis

Programos EM algoritmas

  • Jis gali būti naudojamas pavyzdyje užpildyti trūkstamus duomenis.
  • Jis gali būti naudojamas kaip neprižiūrimo klasterių mokymosi pagrindas.
  • Jis gali būti naudojamas paslėpto Markovo modelio (HMM) parametrams įvertinti.
  • Jis gali būti naudojamas latentinių kintamųjų reikšmėms atrasti.

EM algoritmo privalumai

  • Visada garantuojama, kad tikimybė padidės su kiekviena iteracija.
  • E-step ir M-step dažnai yra gana lengvas daugeliui problemų, susijusių su įgyvendinimu.
  • M žingsnių sprendimai dažnai egzistuoja uždaroje formoje.

EM algoritmo trūkumai

  • Jis turi lėtą konvergenciją.
  • Tai daro konvergenciją tik prie vietinių optimalų.
  • Tam reikia ir tikimybių, tiek pirmyn, tiek atgal (skaitiniam optimizavimui reikia tik į priekį).