A Režisuotas aciklinis grafikas , dažnai sutrumpintas kaip DIENA , yra pagrindinė grafų teorijos sąvoka. DAG naudojami aiškiai ir organizuotai parodyti, kaip dalykai yra susiję arba priklauso vienas nuo kito. Šiame straipsnyje mes sužinosime apie Režisuotas aciklinis grafikas , jo savybės ir pritaikymas realiame gyvenime.

Režisuotas aciklinis grafikas

Kas yra nukreiptas aciklinis grafikas?

A Režisuotas aciklinis grafikas (DAG) yra nukreiptas grafikas, kuriame nėra ciklų.

Žemiau pateikta diagrama vaizduoja nukreiptą aciklinį grafiką (DAG):

Tiesioginis aciklinis grafikas

Nukreipto aciklinio grafiko reikšmė:

Nukreiptas aciklinis grafikas turi dvi svarbias funkcijas:

• Režisuotas Edge'as s:Režisuotame acikliniame grafike, kiekvienas kraštas turi kryptį, tai reiškia, kad jis eina iš vienos viršūnės (mazgo) į kitą. Ši kryptis reiškia a Vienas kelias ryšys arba priklausomybė tarp mazgų.
• Aciklinis: Terminas aciklinis rodo, kad diagramoje nėra ciklų ar uždarų kilpų. Kitaip tariant, negalite pereiti nukreiptų briaunų sekos ir grįžti į tą patį mazgą, vadovaudamiesi krašto kryptimis. Ciklų formavimas draudžiamas DIENA. Todėl ši savybė yra būtina.

Režisuotas aciklinis grafikas

Nukreipto aciklinio grafiko DAG savybės:

Nukreiptas aciklinis grafikas (DAG) turi skirtingas savybes, todėl juos galima naudoti grafiko uždaviniams spręsti.

Yra šios nukreiptos aciklinės grafikos (DAG) savybės:

• Pasiekiamumo santykis: DAG galime nustatyti, ar tarp dviejų mazgų yra pasiekiamumo ryšys. Teigiama, kad mazgas A pasiekiamas iš mazgo B, jei yra nukreiptas kelias, kuris prasideda mazge B ir baigiasi mazge A. Tai reiškia, kad galite sekti grafiko briaunų kryptį, kad patektumėte iš B į A.
• Laikinasis uždarymas: Tranzityvus nukreipto grafiko uždarymas yra naujas grafikas, vaizduojantis visus tiesioginius ir netiesioginius ryšius arba ryšius tarp pradinio grafiko mazgų. Kitaip tariant, jis nurodo, kuriuos mazgus galima pasiekti iš kitų mazgų, laikantis vieno ar kelių nukreiptų kraštų.

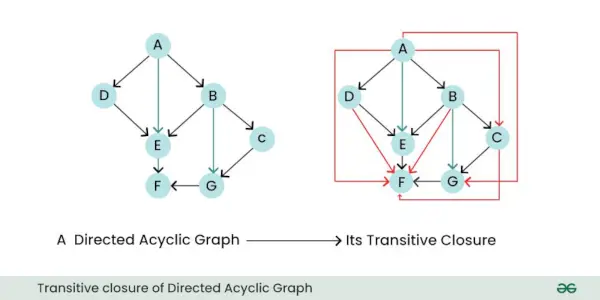
Tranzityvus nukreipto aciklinio grafiko uždarymas

• Tranzityvus sumažinimas: Tranzityvus nukreipto grafo redukavimas yra naujas grafikas, kuris išlaiko tik esminius, tiesioginius ryšius tarp mazgų, pašalindamas bet kokias nereikalingas netiesiogines briaunas. Iš esmės jis supaprastina grafiką, pašalindamas briaunas, kurias galima daryti iš likusių kraštų.

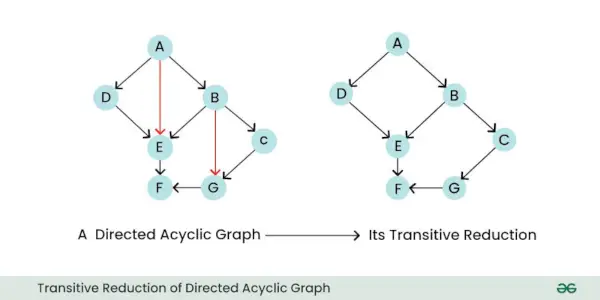
Tranzityvus nukreipto aciklinio grafiko redukcija

• Topologinė tvarka: DAG gali būti surūšiuotas topologiškai, o tai reiškia, kad galite tiesiškai išdėstyti jo mazgus taip, kad visų kraštų pradžios briaunos mazgas atsirastų anksčiau sekoje. Ši nuosavybė naudinga atliekant tokias užduotis kaip planavimas ir priklausomybės sprendimas.

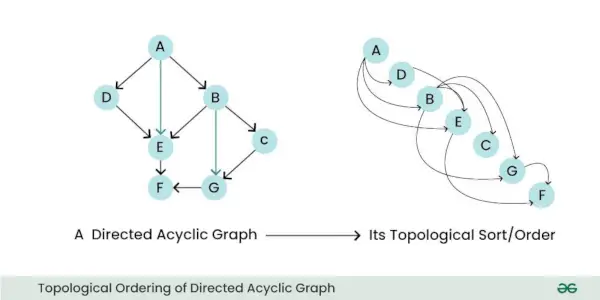
Topologinis nukreipto aciklinio grafiko išdėstymas

Praktiniai DAG pritaikymai:

• Duomenų srauto analizė: Kuriant ir optimizuojant kompiliatorių, DAG naudojami duomenų srautui programoje pavaizduoti. Tai padeda optimizuoti kodą, nustatant perteklinius skaičiavimus ir negyvą kodą. DAG taip pat naudojami struktūrai pavaizduoti pagrindiniai blokai Kompiliatoriaus projekte.

• Užduočių planavimas: DAG naudojami projektų valdymui ir darbų planavimui. Kiekviena užduotis arba darbas yra vaizduojamas kaip mazgas DAG, o nukreiptos briaunos rodo priklausomybes. Aciklinis DAG pobūdis užtikrina, kad užduotys būtų suplanuotos logiška tvarka, užkertant kelią žiedinėms priklausomybėms.

Svertinis nukreiptas aciklinis grafikas gali būti naudojamas planavimo problemai pavaizduoti. Paimkime užduočių planavimo problemos pavyzdį. Čia viršūnė gali reikšti užduotį, o jos svoris – užduoties skaičiavimo dydį. Panašiai briauna gali reikšti ryšį tarp dviejų užduočių, o jo svoris – ryšio išlaidas:

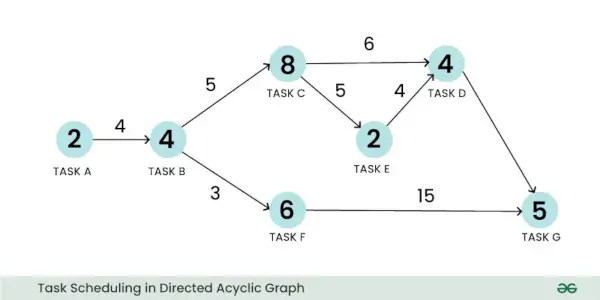
Užduočių planavimas nukreiptame acikliniame grafike

Išvada:

Apibendrinant galima pasakyti, kad nukreipti acikliniai grafikai yra pagrindinė grafų teorijos koncepcija, turinti daugybę praktinių pritaikymų. DAG vaidina lemiamą vaidmenį planuojant užduotis, analizuojant duomenų srautus, sprendžiant priklausomybę ir įvairiose kitose kompiuterių mokslo ir inžinerijos srityse. Jie padeda optimizuoti procesus, valdyti priklausomybes ir užtikrinti efektyvų užduočių ar darbų vykdymą.