Kas yra Circular susietas sąrašas?
The apskritas susietas sąrašas yra susietas sąrašas, kuriame visi mazgai yra sujungti, kad sudarytų apskritimą. Apskritame susietame sąraše pirmasis ir paskutinis mazgas yra sujungti vienas su kitu, o tai sudaro apskritimą. Pabaigoje nėra NULL.
Aplinkinis susietas sąrašas
Paprastai yra dviejų tipų žiediniai susietieji sąrašai:
- Apvalus atskirai susietas sąrašas: Apvaliame atskirai susietame sąraše paskutiniame sąrašo mazge yra žymeklis į pirmąjį sąrašo mazgą. Perkeliame apskritą atskirai susietą sąrašą, kol pasiekiame tą patį mazgą, nuo kurio pradėjome. Apvalus atskirai susietas sąrašas neturi pradžios ar pabaigos. Kitoje bet kurio mazgo dalyje nėra nulinės reikšmės.
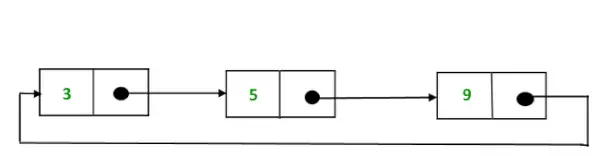
Circular atskirai susieto sąrašo atvaizdavimas
- Circular Dvigubai susietas sąrašas: Apskritasis dvigubai susietas sąrašas turi ir dvigubai susieto sąrašo, ir apskrito susieto sąrašo ypatybes, kuriose du iš eilės elementai yra susieti arba sujungti ankstesne ir kita žymekliu, o paskutinis mazgas nukreipia į pirmąjį mazgą pagal kitą žymeklį, o pirmasis mazgas nurodo į paskutinis mazgas pagal ankstesnį žymeklį.
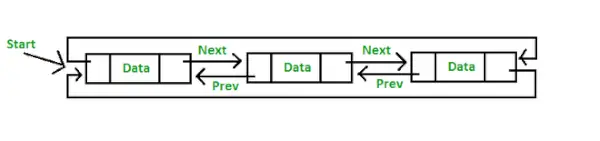
Apvalaus dvigubai susieto sąrašo vaizdavimas
masyvo sąrašas surūšiuotas
Pastaba: Mes naudosime pavienį apskritą susietą sąrašą, kad pavaizduotume apskrito susieto sąrašo veikimą.
Apvalaus susieto sąrašo vaizdavimas:
Žiediniai susieti sąrašai yra panašūs į atskirus susietus sąrašus, išskyrus paskutinio mazgo sujungimą su pirmuoju mazgu.
Apvalaus susieto sąrašo mazgo atvaizdas:
C++ // Class Node, similar to the linked list class Node{ int value; // Points to the next node. Node next; }> C struct Node { int data; struct Node *next; };> Java public class Node { int data; Node next; public Node(int data) { this.data = data; this.next = null; } }> C# public class Node { public int data; public Node next; public Node(int data) { this.data = data; this.next = null; } }> Javascript class Node { constructor(data) { this.data = data; this.next = null; } }> PHP class Node { public $data; public $next; function __construct($data) { $this->duomenys = $duomenys; $šis->kitas = null; } }>>Python3Apskritojo atskirai susieto sąrašo pavyzdys:10 iki 6 laipsnio

Apvalaus susieto sąrašo pavyzdys
Aukščiau pateiktas atskirai susietas apskritojo rašto sąrašas gali būti pavaizduotas kaip:
C++ // Initialize the Nodes. Node one = new Node(3); Node two = new Node(5); Node three = new Node(9); // Connect nodes one.next = two; two.next = three; three.next = one;>
C Node* one = createNode(3); Node* two = createNode(5); Node* three = createNode(9); // Connect nodes one->kitas = du; du->kitas = trys; trys->kitas = vienas;>>
Java Node one = new Node(3); Node two = new Node(5); Node three = new Node(9); // Connect nodes one.next = two; two.next = three; three.next = one;>
Javascript let one = new Node(3); let two = new Node(5); let three = new Node(9); // Connect nodes one.next = two; two.next = three; three.next = one;>
PHP $one = new Node(3); $two = new Node(5); $three = new Node(9); // Connect nodes $one->kitas = $ du; $dvi->kitas = $trys; $trys->kitas = $vienas;>>Python3 Paaiškinimas: Aukščiau pateiktoje programoje vienas, du ir trys yra mazgas su atitinkamai 3, 5 ir 9 reikšmėmis, kurie yra sujungti apskritimu taip: - „Node One“: Kitas žymeklis saugo antrojo mazgo adresą.
- Antrajam mazgui: Kitas saugo trečiojo mazgo adresą
- Trečiam mazgui: The Kitas nukreipia į mazgą vienas.
Veiksmai apskritime susietame sąraše:
Mes galime atlikti kai kurias operacijas su žiediniu susietu sąrašu, panašiu į atskirai susietą sąrašą, kurios yra:
- Įdėjimas
- Ištrynimas
1. Įterpimas į žiedinį susietą sąrašą:
Mazgą galima pridėti trimis būdais:
- Įterpimas sąrašo pradžioje
- Įterpimas sąrašo pabaigoje
- Įterpimas tarp mazgų
1) Įterpimas sąrašo pradžioje: Norėdami įterpti mazgą sąrašo pradžioje, atlikite šiuos veiksmus:
- Sukurkite mazgą, pasakykite T.
- Padaryti T -> kitas = paskutinis -> kitas.
- paskutinis -> kitas = T.
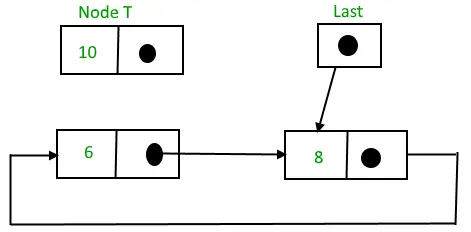
Apvalus susietas sąrašas prieš įterpiant
Ir tada,
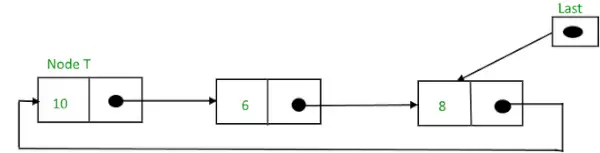
Apvalus susietas sąrašas po įterpimo
2) Įterpimas sąrašo pabaigoje: Norėdami įterpti mazgą sąrašo pabaigoje, atlikite šiuos veiksmus:
- Sukurkite mazgą, pasakykite T.
- Padaryti T -> kitas = paskutinis -> kitas;
- paskutinis -> kitas = T.
- paskutinis = T.
Prieš įdėdami,
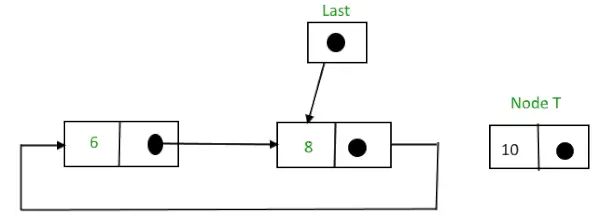
Apvalus susietas sąrašas prieš įterpiant mazgą pabaigoje
eilutė pakeisti visą java
Po įdėjimo,
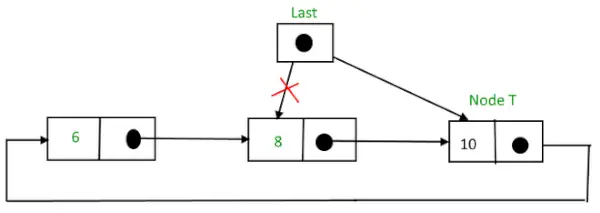
Apvalus susietas sąrašas po mazgo įterpimo pabaigoje
3) Įterpimas tarp mazgų: Norėdami įterpti mazgą tarp dviejų mazgų, atlikite šiuos veiksmus:
- Sukurkite mazgą, pasakykite T.
- Ieškokite mazgo, po kurio reikia įterpti T, pasakykite, kad mazgas yra P.
- Padaryti T -> kitas = P -> kitas;
- P -> kitas = T.
Tarkime, kad 12 reikia įterpti po to, kai mazgas turi 10 reikšmę,
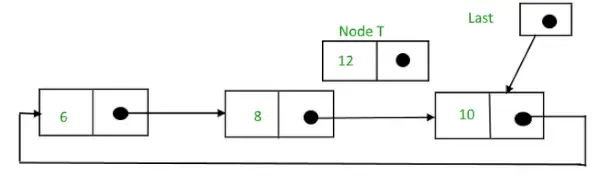
Apvalus susietas sąrašas prieš įterpiant
Po paieškos ir įterpimo,
abstraktūs metodai
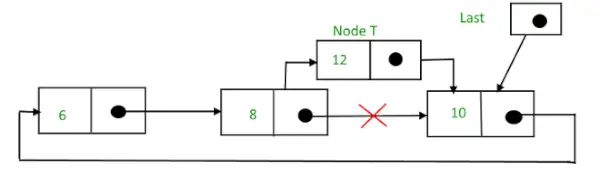
Apvalus susietas sąrašas po įterpimo
2. Ištrynimas žiediniame susietame sąraše:
1) Ištrinkite mazgą tik tuo atveju, jei jis yra vienintelis mazgas žiediniame susietame sąraše:
- Atlaisvinkite mazgo atmintį
- Paskutinė reikšmė turi būti NULL Mazgas visada nurodo kitą mazgą, todėl NULL priskyrimas nebūtinas.
Bet kurį mazgą galima nustatyti kaip pradžios tašką.
Mazgai greitai perkeliami nuo pirmojo iki paskutinio.
2) Paskutinio mazgo ištrynimas:
- Raskite mazgą prieš paskutinį mazgą (tegul jis būna temp)
- Laikykite mazgo adresą šalia paskutinio mazgo temp
- Ištrinkite paskutinę atmintį
- Pabaigoje įdėkite temp
3) Ištrinkite bet kurį mazgą iš apskrito susieto sąrašo: Mums bus suteiktas mazgas, o mūsų užduotis yra ištrinti tą mazgą iš apskrito susieto sąrašo.
Algoritmas:
1 atvejis : Sąrašas tuščias.
localdate java
- Jei sąrašas tuščias, mes tiesiog grįšime.
2 atvejis :Sąrašas nėra tuščias
- Jei sąrašas nėra tuščias, mes apibrėžiame du rodiklius curr ir ankstesnė ir inicijuokite žymeklį curr su galva mazgas.
- Pereikite sąrašą naudodami curr norėdami rasti mazgą, kurį reikia ištrinti, ir prieš pereinant prie curr į kitą mazgą, kiekvieną kartą nustatykite prev = curr.
- Jei mazgas rastas, patikrinkite, ar tai vienintelis mazgas sąraše. Jei taip, nustatykite head = NULL ir free (curr).
- Jei sąraše yra daugiau nei vienas mazgas, patikrinkite, ar tai pirmasis sąrašo mazgas. Sąlyga tai patikrinti (curr == galva). Jei taip, pereikite prie ankstesnio, kol pasieks paskutinį mazgą. Kai ankstesnis pasiekia paskutinį mazgą, nustatykite head = head -> next ir prev -> next = head. Ištrinti curr.
- Jei curr nėra pirmasis mazgas, patikriname, ar tai paskutinis mazgas sąraše. Sąlyga norint tai patikrinti yra (curr -> next == head).
- Jei curr yra paskutinis mazgas. Nustatykite ankstesnį -> kitą = head ir ištrinkite mazgą curr naudodami free(curr).
- Jei mazgas, kurį reikia ištrinti, nėra nei pirmasis, nei paskutinis mazgas, nustatykite ankstesnį -> kitą = curr -> next ir ištrinkite curr.
- Jei mazgo sąraše nėra, grąžinkite galvą ir nieko nedarykite.
Toliau pateikiamas pirmiau nurodyto metodo įgyvendinimas:
C++ // C++ program to delete a given key from // linked list. #include using namespace std; // Structure for a node class Node { public: int data; Node* next; }; // Function to insert a node at the // beginning of a Circular linked list void push(Node** head_ref, int data) { // Create a new node and make head // as next of it. Node* ptr1 = new Node(); ptr1->duomenys = duomenys; ptr1->kitas = *head_ref; // Jei susieto sąrašo reikšmė nėra NULL, tada // nustatykite kitą iš paskutinio mazgo if (*head_ref != NULL) { // Raskite mazgą prieš head ir // atnaujinkite šalia jo. Mazgas* temp = *head_ref; while (temp->ext != *head_ref) temp = temp->ext; temp->kitas = ptr1; } else // Pirmajam mazgui ptr1->next = ptr1; *head_ref = ptr1; } // Funkcija spausdinti mazgus duotame // apskrito susieto sąrašo void printList(Node* head) { Node* temp = head; if (head != NULL) { do { cout<< temp->duomenis<< ' '; temp = temp->Kitas; } while (temp != galva); } cout<< endl; } // Function to delete a given node // from the list void deleteNode(Node** head, int key) { // If linked list is empty if (*head == NULL) return; // If the list contains only a // single node if ((*head)->duomenys == raktas && (*head)->kitas == *head) { free(*head); *galva = NULL; grąžinti; } Mazgas *paskutinis = *galva, *d; // Jei head turi būti ištrintas if ((*head)->data == raktas) { // Rasti paskutinį sąrašo mazgą while (last->next != *head) last = paskutinis->ext; // Nukreipkite paskutinį mazgą į kitą // head ty antrąjį sąrašo mazgą // last->ext = (*head)->ext; laisvas(*galva); *galva = paskutinis->kitas; grąžinti; } // Arba norimas ištrinti mazgas // nerastas arba sąrašo pabaiga // nepasiekta, kol (paskutinis->kitas != *head && last->ext->data != key) { paskutinis = paskutinis ->kitas; } // Jei mazgas, kurį reikia ištrinti, buvo rastas if (paskutinis->kitas->duomenys == raktas) { d = paskutinis->kitas; paskutinis->kitas = d->kitas; laisvas(d); } dar cout<< 'Given node is not found in the list!!!
'; } // Driver code int main() { // Initialize lists as empty Node* head = NULL; // Created linked list will be // 2->5->7->8->10 stūmimų(&galva, 2); stumti(&galva, 5); stumti(&galva, 7); stumti(&galva, 8); stumti(&galva, 10); cout<< 'List Before Deletion: '; printList(head); deleteNode(&head, 7); cout << 'List After Deletion: '; printList(head); return 0; }> C #include #include // Structure for a node struct Node { int data; struct Node* next; }; // Function to insert a node at the // beginning of a Circular linked list void push(struct Node** head_ref, int data) { // Create a new node and make head // as next of it. struct Node* ptr1 = (struct Node*)malloc(sizeof(struct Node)); ptr1->duomenys = duomenys; ptr1->kitas = *head_ref; // Jei susieto sąrašo reikšmė nėra NULL, tada // nustatykite kitą iš paskutinio mazgo if (*head_ref != NULL) { // Raskite mazgą prieš head ir // atnaujinkite šalia jo. struct Mazgas* temp = *head_ref; while (temp->ext != *head_ref) temp = temp->ext; temp->kitas = ptr1; } else // Pirmajam mazgui ptr1->next = ptr1; *head_ref = ptr1; } // Funkcija spausdinti mazgus duotame // apskrito susieto sąrašo void printList(struct Node* head) { struct Node* temp = head; if (head != NULL) { do { printf ('%d ', temp-> data); temp = temp->kitas; } while (temp != galva); } printf('
'); } // Funkcija ištrinti duotą mazgą // iš sąrašo void deleteNode(struct Node** head, int key) { // Jei susietas sąrašas tuščias if (*head == NULL) return; // Jei sąraše yra tik // vienas mazgas if ((*head)->data == key && (*head)->ext == *head) { free(*head); *galva = NULL; grąžinti; } struct Mazgas *paskutinis = *galva, *d; // Jei head turi būti ištrintas if ((*head)->data == raktas) { // Rasti paskutinį sąrašo mazgą while (last->next != *head) last = paskutinis->ext; // Nukreipkite paskutinį mazgą į kitą // head ty antrąjį sąrašo mazgą // last->ext = (*head)->ext; laisvas(*galva); *galva = paskutinis->kitas; grąžinti; } // Arba norimas ištrinti mazgas // nerastas arba sąrašo pabaiga // nepasiekta, kol (paskutinis->kitas != *head && last->ext->data != key) { paskutinis = paskutinis ->kitas; } // Jei mazgas, kurį reikia ištrinti, buvo rastas if (paskutinis->kitas->duomenys == raktas) { d = paskutinis->kitas; paskutinis->kitas = d->kitas; laisvas(d); } else printf('Duotas mazgas sąraše nerastas!!!
'); } // Tvarkyklės kodas int main() { // Inicijuoti sąrašus kaip tuščią struktūrą Mazgas* head = NULL; // Sukurtas susietas sąrašas bus // 2->5->7->8->10 push(&head, 2); stumti(&galva, 5); stumti(&galva, 7); stumti(&galva, 8); stumti(&galva, 10); printf('Sąrašas prieš ištrynimą: '); printList(head); deleteNode(&head, 7); printf('Sąrašas po ištrynimo: '); printList(head); grąžinti 0; }> Java // Java program to delete a given key from // linked list. import java.io.*; import java.util.*; public class GFG { /* structure for a node */ static class Node { int data; Node next; }; /* Function to insert a node at the beginning of a Circular linked list */ static Node push(Node head_ref, int data) { // Create a new node and make head as next // of it. Node ptr1 = new Node(); ptr1.data = data; ptr1.next = head_ref; /* If linked list is not null then set the next of last node */ if (head_ref != null) { // Find the node before head and update // next of it. Node temp = head_ref; while (temp.next != head_ref) temp = temp.next; temp.next = ptr1; } else ptr1.next = ptr1; /*For the first node */ head_ref = ptr1; return head_ref; } /* Function to print nodes in a given circular linked list */ static void printList(Node head) { Node temp = head; if (head != null) { do { System.out.printf('%d ', temp.data); temp = temp.next; } while (temp != head); } System.out.printf('
'); } /* Function to delete a given node from the list */ static Node deleteNode(Node head, int key) { if (head == null) return null; int flag = 0; // Find the required node Node curr = head, prev = new Node(); while (curr.data != key) { if (curr.next == head) { System.out.printf( 'Given node is not found in the list!!!
'); flag = 1; break; } prev = curr; curr = curr.next; } // Check if the element is not present in the list if (flag == 1) return head; // Check if node is only node if (curr == head && curr.next == head) { head = null; return head; } // If more than one node, check if // it is first node if (curr == head) { prev = head; while (prev.next != head) prev = prev.next; head = curr.next; prev.next = head; } // check if node is last node else if (curr.next == head) { prev.next = head; } else { prev.next = curr.next; } return head; } /* Driver code */ public static void main(String args[]) { /* Initialize lists as empty */ Node head = null; /* Created linked list will be 2.5.7.8.10 */ head = push(head, 2); head = push(head, 5); head = push(head, 7); head = push(head, 8); head = push(head, 10); System.out.printf('List Before Deletion: '); printList(head); head = deleteNode(head, 7); System.out.printf('List After Deletion: '); printList(head); } } // This code is contributed by Susobhan Akhuli> C# using System; // Structure for a node public class Node { public int data; public Node next; } // Class for Circular Linked List public class CircularLinkedList { // Function to insert a node at the // beginning of a Circular linked list public static void Push(ref Node head_ref, int data) { // Create a new node and make head // as next of it. Node ptr1 = new Node(); ptr1.data = data; ptr1.next = head_ref; // If linked list is not NULL then // set the next of last node if (head_ref != null) { // Find the node before head and // update next of it. Node temp = head_ref; while (temp.next != head_ref) temp = temp.next; temp.next = ptr1; } else // For the first node ptr1.next = ptr1; head_ref = ptr1; } // Function to print nodes in a given // circular linked list public static void PrintList(Node head) { Node temp = head; if (head != null) { do { Console.Write(temp.data + ' '); temp = temp.next; } while (temp != head); } Console.WriteLine(); } // Function to delete a given node // from the list public static void DeleteNode(ref Node head, int key) { // If linked list is empty if (head == null) return; // If the list contains only a // single node if (head.data == key && head.next == head) { head = null; return; } Node last = head, d; // If head is to be deleted if (head.data == key) { // Find the last node of the list while (last.next != head) last = last.next; // Point last node to the next of // head i.e. the second node // of the list last.next = head.next; head = last.next; return; } // Either the node to be deleted is // not found or the end of list // is not reached while (last.next != head && last.next.data != key) { last = last.next; } // If node to be deleted was found if (last.next.data == key) { d = last.next; last.next = d.next; } else Console.WriteLine( 'Given node is not found in the list!!!'); } // Driver code public static void Main() { // Initialize lists as empty Node head = null; // Created linked list will be // 2->5->7->8->10 stūmimas (galva, 2); Stūmimas(galvutė, 5); Stūmimas (galvutė, 7); Stumti(galvytė, 8); Stūmimas(galva, 10); Console.Write('Sąrašas prieš ištrynimą: '); SpausdintiSąrašas(galva); DeleteNode(nuorodos galvutė, 7); Console.Write('Sąrašas po ištrynimo: '); SpausdintiList(head); } }>> Javascript5->7->8->10 galvos = stumti(galva, 2); galva = stumti(galva, 5); galva = stumti(galva, 7); galva = stumti(galva, 8); galva = stumti(galva, 10); console.log('Sąrašas prieš ištrynimą: '); printList(head); ištrintiMazgas(galva, 7); console.log('Sąrašas po ištrynimo: '); printList(head);>> Python35->7->8->10 galvos = stumti(galva, 2) galva = stumti(galva, 5) galva = stumti(galva, 7) galva = stumti(galva, 8) galva = stumti(galva, 10) print('List Before Deletion: ') printList(head) deleteMazgas(head, 7) print('Sąrašas po ištrynimo: ') printList(head)>
Išvestis
List Before Deletion: 10 8 7 5 2 List After Deletion: 10 8 5 2>
Laiko sudėtingumas: O(N), Blogiausias atvejis įvyksta, kai elementas, kurį reikia ištrinti, yra paskutinis ir mes turime pereiti per visą sąrašą.
Pagalbinė erdvė: O(1), kaip pastovi naudojama papildoma erdvė.
Žiedinių susietų sąrašų pranašumai:
- Bet koks mazgas gali būti atskaitos taškas. Mes galime pereiti visą sąrašą, pradėdami nuo bet kurio taško. Mums tereikia sustoti, kai vėl aplankomas pirmasis aplankytas mazgas.
- Naudinga diegiant eilę. Skirtingai nei tai įgyvendinimui, mums nereikia išlaikyti dviejų rodyklių priekyje ir gale, jei naudojame apskritą susietą sąrašą. Mes galime išlaikyti žymeklį į paskutinį įterptą mazgą, o priekinę dalį visada galima gauti kaip kitą iš paskutinio.
- Apvalūs sąrašai yra naudingi programose, norint pakartotinai apeiti sąrašą. Pavyzdžiui, kai kompiuteryje veikia kelios programos, įprasta, kad operacinė sistema įtraukia veikiančias programas į sąrašą, tada jas peržiūri, suteikdama kiekvienai iš jų šiek tiek laiko paleisti, o tada priversdama jas laukti. CPU perduodamas kitai programai. Operacinei sistemai patogu naudoti apskritą sąrašą, kad, pasiekusi sąrašo pabaigą, ji galėtų judėti sąrašo priekyje.
- Apvalūs dvigubai susieti sąrašai naudojami pažangioms duomenų struktūroms, tokioms kaip Fibonačio krūva .
- Palyginti su kitomis sudėtingesnėmis duomenų struktūromis, pvz., medžiais ar grafikais, sudaryti žiedinį susietą sąrašą gali būti gana paprasta.
Apvalaus susieto sąrašo trūkumai:
- Palyginti su atskirais susietais sąrašais, žiediniai sąrašai yra sudėtingesni.
- Apvalaus sąrašo atsukimas yra sudėtingesnis nei vienkartinis ar dvigubas apskrito sąrašo atsukimas.
- Kodas gali patekti į begalinę kilpą, jei su juo nebus elgiamasi atsargiai.
- Sunkiau rasti sąrašo pabaigą ir valdyti kilpą.
- Nors žiediniai susieti sąrašai gali būti veiksmingi tam tikrose programose, tam tikrais atvejais jų veikimas gali būti lėtesnis nei kitų duomenų struktūrų, pavyzdžiui, kai sąrašą reikia rūšiuoti arba ieškoti.
- Žiediniai susieti sąrašai nesuteikia tiesioginės prieigos prie atskirų mazgų
Apvalių susietų sąrašų taikymas:
- Kelių žaidėjų žaidimai naudoja tai, kad kiekvienas žaidėjas turėtų galimybę žaisti.
- Apvalus susietas sąrašas gali būti naudojamas kelioms operacinėje sistemoje veikiančioms programoms organizuoti. Šias programas kartoja OS.
- Apvalūs susieti sąrašai gali būti naudojami sprendžiant išteklių paskirstymo problemas.
- Žiediniai susieti sąrašai dažniausiai naudojami žiediniams buferiams įdiegti,
- Apvalūs susieti sąrašai gali būti naudojami modeliuojant ir žaidžiant.
Kodėl cirkuliacinis susietas sąrašas?
- Mazgas visada nurodo kitą mazgą, todėl NULL priskyrimas nebūtinas.
- Bet kurį mazgą galima nustatyti kaip pradžios tašką.
- Mazgai greitai perkeliami nuo pirmojo iki paskutinio.
Kiti pranešimai: Aplinkinis susietas sąrašas | 2 rinkinys (perėjimas) Apvalus atskirai susietas sąrašas | Įdėjimas Rašykite komentarus, jei radote klaidų aukščiau esančiame kode/algoritme arba raskite kitų būdų, kaip išspręsti tą pačią problemą






