Trikampio centras yra visų trijų trikampio kampų bisektorių susikirtimo taškas. Centras yra svarbus trikampio taškas, kuriame susijungia linijos, perpjaunančios kampus per pusę. Šis taškas taip pat yra apskritimo, vadinamo Incircle, kuris puikiai telpa trikampio viduje ir vienodai liečia visas tris kraštines, centras. Šiame straipsnyje aptariamos įvairios trikampio centro sąvokos, pvz., kodėl šis taškas svarbus, kaip jį rasti naudojant kompasą ar skaičius ir apskritimo centro ypatybės.
Turinys
- Kas yra trikampio centras?
- Trikampio centro savybės
- Trikampio formulės centras
- Kaip rasti trikampio centrą
- Centroid, Circumcenter, Incenter, Orthocenter
Kas yra trikampio centras?
Trikampio centras, kaip rodo pavadinimas, yra trikampio vidurio taškas. Šis taškas, kurį vadiname centru, susidaro sankryžoje, kur susitinka visos linijos, dalijančios vidinius kampus. Taško atstumas nuo visų trijų trikampio kraštinių yra vienodas. Trikampio apskritimas taip pat puikiai tinka trikampio viduje esančiam apskritimui ir šis apskritimas vadinamas trikampio apskritimu.
Incento apibrėžimas
Trikampio centras yra taškas trikampio viduje, kur susijungia visos trys linijos, perpjaunančios jo vidinius kampus per pusę. Šis taškas yra tokiu pat atstumu nuo trijų trikampio kraštinių, todėl jis panašus į trikampio vidurį. Tai taip pat yra didžiausio apskritimo, kuris gali tvirtai tilpti į trikampį, kurį vadiname apskritimu, centras. Norėdami simbolizuoti centrą, paprastai naudojame raidę I,
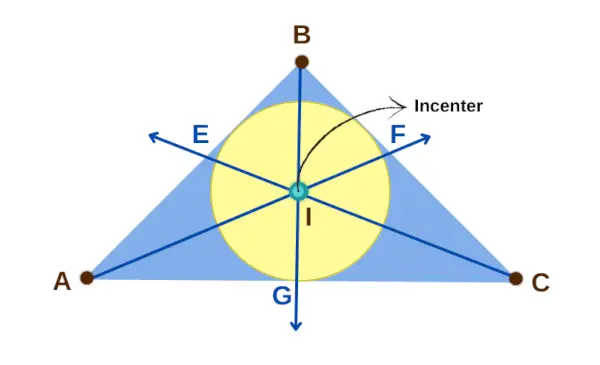
Trikampio centras
Trikampio centro savybės
Kai kurios svarbios trikampio centro savybės yra pateiktos žemiau:
1 nuosavybė: Jeigu aš yra trikampio ABC centras, tada trys poros tiesių atkarpų yra vienodo ilgio: AE ir AG, CG ir CF bei BF ir BE. Tai reiškia, kad AE = AG, CG = CF ir BF = BE.
2 nuosavybė: Centras aš taip pat turi ypatingą ryšį su trikampio kampais. Dėl to kampai ∠BAI ir ∠CAI yra lygūs, ∠BCI ir ∠ACI yra lygūs, o ∠ABI ir ∠CBI yra lygūs. Tai seka kampo bisektoriaus teoremą.
3 nuosavybė: Centras aš yra apskritimo, kuris liečia visas tris trikampio kraštines, centras ir atstumai nuo aš iki trikampio kraštinių (EI, FI, GI) yra vienodi. Šie atstumai vadinami apskritimo spinduliu arba apskritimo spinduliu.
4 nuosavybė: Trikampio plotą galite apskaičiuoti naudodami pusperimetrą (s) ir spindulią (r). Formulė yra A = sr, kur A yra plotas, s yra pusperimetras (s = (a + b + c)/2, kur a, b ir c yra trikampio kraštinių ilgiai), o r yra spindulys.
5 nuosavybė: Trikampio centras visada lieka trikampio viduje. Skirtingai nuo stačiakampio, kuris kai kuriais atvejais gali būti už trikampio ribų, centras visada yra trikampio ribose.
Trikampio formulės centras
Formulė, skirta rasti formulės vidurį su 3 koordinatėmis (x1, ir1), (x2, ir2), ir (x3, ir3) yra:
{(kirvis 1 + bx 2 + cx 3 )/(a + b + c), (yra 1 + pagal 2 + c 3 )/(a + b + c)}
kuriais metais išrastas kompiuteris
Paprastais žodžiais tariant, norėdami gauti centrą, jūs:
- Padauginkite taško A x koordinatę iš kraštinės ilgio a, taško B x koordinatę iš kraštinės ilgio b ir taško C x koordinatę iš kraštinės ilgio c. Tada pridėkite juos kartu.
- Padalinkite rezultatą iš kraštinių ilgių a, b ir c sumos.
- Pakartokite tą patį procesą su y koordinatėmis, bet naudodami kraštinių ilgius a, b ir c.
Trikampio kampo formulės centras
Formulė trikampio kampo centrui rasti yra tokia:
Tegu, trikampyje D, F ir G yra taškai, kuriuose atitinkamai kampų A, B ir C kampų pusiausvyros susikerta su kraštinėmis BC, AC ir AB.
Kampą ∠AIB (kur I yra trikampio centras) galima apskaičiuoti naudojant formulę:
∠AIB = 180° – (pusė kampų A ir B sumos)
ARBA
∠AIB = 180° – (∠A + ∠B)/2
Kaip rasti trikampio centrą
Yra du būdai, kaip rasti trikampio centrą. Statyboje mes nustatome įcentrą, nubrėždami trikampio kampo pusiausvyras. Koordinačių geometrijoje mes naudojame formulę centrui nustatyti.
Koordinačių geometrijos naudojimas : Raskite trikampio centrą, kurio koordinatės pateiktos kaip: A(2, 2), B(6, 2) ir C(4, 5)
Pagal pateiktą informaciją
- (x1, ir1) = (2, 2)
- (x2, ir2) = (6, 2)
- (x3, ir3) = (4, 5)
Mes žinome, kad trikampio centras yra:
I(x, y) = {(kirvis 1 + bx 2 + cx 3 )/(a + b + c), (yra 1 + pagal 2 + c 3 )/(a + b + c)}
A pusei: atstumas tarp taškų B ir C = √((6 – 4)2+ (2–5)2) = √8
Kraštinei b: atstumas tarp taškų A ir C = √((2–4)2+ (2–5)2) = √13
Kraštinei c: atstumas tarp taškų A ir B = √((6 – 2)2+ (2–2)2) = 4
Įtraukę a, b, c reikšmes į centro formulę, gauname:
I(x, y) = {(8 × 2 + 13 × 5 + 4 × 4) / (8 + 13 +4), (8 × 2 + 13 × 2 + 4 × 5) / (8 + 13 +4 )}
⇒ I(x, y) = (16 + 78 + 16)/(25), (16 + 26 + 20)/(25)
⇒ I(x, y) = (110/25, 62/25) = (22/5,62/25)
∴ Trikampio ABC centras su koordinatėmis yra (22/5,62/25)
Pete'o Davidsono pilietybė
Kaip sukurti trikampio centrą?
Norint sukurti trikampio centrą, reikės naudoti kompasą. Naudodami kompasą atlikite toliau nurodytus veiksmus.
1 žingsnis: Uždėkite vieną kompaso galą ant trikampio viršūnės, o kitas galas liečia vieną kraštą.
2 žingsnis: Kompasu nubrėžkite du lankus dviejose trikampio pusėse.
3 veiksmas: Tuo pačiu atstumu ant kompaso padarykite du lankus trikampio viduje. Šie lankai turėtų kirsti vienas kitą nuo tos vietos, kur jie liečiasi su šonais.
4 veiksmas: Nubrėžkite liniją nuo trikampio viršūnės iki dviejų vidinių lankų susikerta.
5 veiksmas: Pakartokite tuos pačius veiksmus iš kitos trikampio viršūnės.
6 veiksmas: Vieta, kur susikerta arba susikerta dvi linijos, yra trikampio centras.
Stačiakampio trikampio centras
Centras, jei a Stačiakampis trikampis yra taškas, kuriame susikerta visos stačiojo kampo trikampio kampų pusiausvyros. Jei stačiojo trikampio kraštinės matuoja a, b ir c, tada apskritimo „r“ spindulys pateikiamas kaip r = (ab)/(a + b + c). Stačiojo trikampio vidurys pavaizduotas žemiau:
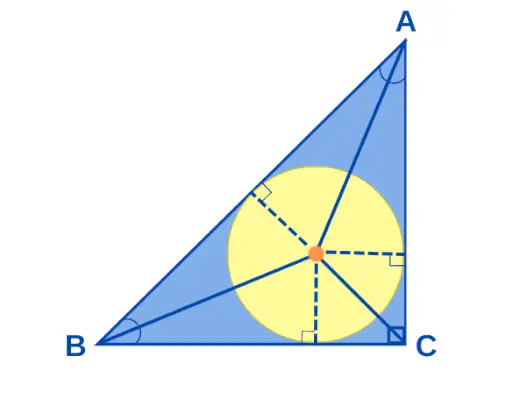
Stačiakampio trikampio centras
tipas java
Centroid, Circumcenter, Incenter, Orthocenter
Centroid, Circumcenter, Incenter ir Orthocenter yra keturi svarbūs taškai, susiję su traingle. Žemiau pateikiamas Centroid, Circumcenter, Incenter ir Orthocenter palyginimas:
Centroidas | Aplink centrą | Incenteris | Ortocentras |
|---|---|---|---|
Medianos susikirtimo taškas | Statmens bisektoriaus susikirtimo taškas | Kampo bisektoriaus susikirtimo taškas | Aukščių susikirtimo taškas |
Medianą dalija 2:1 | Trikampio apskritimo centras | Trikampio apskritimo centras | Stačiakampio trikampio stačiakampis yra stačiu kampu |
Taip pat patikrinkite
css teksto įvyniojimui
- Trikampio plotas
- Trikampio perimetras
- Trikampio kampo sumos savybė
Trikampio centravimo pavyzdžiai
1 pavyzdys: Apskaičiuokite trikampio ABC vidurį. AB= 8cm, BC= 15 cm, CA= 17 cm.
Sprendimas:
Naudojant trikampio vidurio formulę = (aA + bB + cC)/(a + b + c)
kur,
- a = 8
- b = 15
- c = 17
O kampai yra,
- A = 30°
- B = 60°
- C = 90°
Įdėjus šias vertes į formulę,
⇒ {(8)(30) + (15)(60) + (17)(90)}/{8 + 15 + 17}
⇒ (240 + 900 + 1530)/40
⇒ 2670/40
⇒ 66,75
2 pavyzdys: Jane apskaičiavo trikampio lauko plotą kaip 120 kvadratinių metrų. Lauko perimetras yra 36 metrai. Jei trikampio viduje nubrėžtas apskritimas taip, kad jis liestų kiekvieną trikampio kraštinę, padėkite Džeinei apskaičiuoti trikampio spindulį.
Sprendimas:
Pagal pateiktą informaciją,
Trikampio plotas = 120 kvadratinių metrų
Trikampio perimetras = 36 metrai
Mes žinome, kad trikampio plotas = r × s
s = pusperimetras
s = p/2 = 36/2 = 18
A = r × s
r = A/s
r = 120/18
r = 6,67 metro
Praktikos uždaviniai trikampio centre
1 uždavinys: duotas trikampis PQR su viršūnėmis P(1, 2), Q(4, 6) ir R(7, 2), raskite centro koordinates.
2 uždavinys. Sukurkite trikampį ABC, kurio ∠A = 45°, ∠B = 60° ir ∠C = 75°. Norėdami rasti centrą, naudokite konstravimo metodą.
3 uždavinys: trikampyje LMN, jei ∠L = 75°, ∠M = 60° ir ∠N = 45°, suraskite centro koordinates.
4 uždavinys. Sukurkite trikampį XYZ, kurio ∠X = 80°, ∠Y = 50° ir ∠Z = 50°. Norėdami rasti centrą, naudokite konstravimo metodą.
Trikampio centras: DUK
Kas yra trikampio centras?
Trikampio centras yra taškas, kuriame susikerta vidinių kampų pusiausvyros. Jis yra vienodu atstumu nuo visų trijų trikampio kraštinių.
konvertuoti eilutę į sveikąjį skaičių
Kokia yra trikampio centro reikšmė?
Centras yra reikšmingas, nes tai yra trikampio apskritimo centras, didžiausias apskritimas, kuris telpa trikampio viduje. Jis turi savybę būti vienodu atstumu nuo visų pusių.
Ar Incentas gali būti už trikampio ribų?
Ne, centras visada yra trikampio viduje. Tai kampo bisektorių sutapimo taškas ir pagal apibrėžimą jis turi būti trikampio ribose.
Kaip incenteris sukonstruotas naudojant kompasą ir tiesią briauną?
Norėdami sukurti įcentrą, naudokite kompasą, kad iš kiekvienos viršūnės į priešingą pusę nubrėžtumėte kampo pusiausvyras. Centras yra taškas, kuriame šie bisektoriai susikerta.
Kas yra „Incenter Formula“?
Trikampio įbrėžimo formulė gali būti parašyta taip:
frac{(aA+bB+cC)}{a+b+c}
Kokios yra trikampio centro savybės?
Centras turi keletą pagrindinių savybių. Jis yra vienodu atstumu nuo trikampio kraštinių, o tai reiškia, kad atstumai iki kraštinių yra vienodi. Be to, tai yra kampų bisektorių susikirtimo taškas, padalijantis kampus į dvi lygias dalis.
Kaip nustatomas centras?
Norėdami nustatyti įcentrą, turite rasti kampo bisektorių susikirtimo vietą. Tai galima padaryti naudojant įcentrinę formulę arba nubrėžus kampo bisektorius ir surandant jų susikirtimo tašką.
Kuo skiriasi Incentre ir Circumcentre?
Pagrindinis skirtumas tarp incenter ir circumcenter yra jų dėmesys. Įcentrinis taškas susijęs su kampo bisektriais ir yra įbrėžto apskritimo centras, o cirkumcentras susijęs su statmenais bisektoriais ir yra apibrėžtojo apskritimo centras.
Ar Incentre ir Centroid yra tas pats?
Ne, centras ir centroidas skiriasi. Centras yra ta vieta, kur susikerta kampo pusiausvyros, o centroidas yra ta vieta, kur susikerta medianos. Medianos jungia viršūnes su priešingos pusės vidurio tašku.
Ar Incentre ir Orthocentre yra tas pats?
Ne, centras ir ortocentras nėra tas pats. Centras yra taškas, kuriame kampas dalija vienas kitą, o ortocentras apima aukštis - tieses iš kiekvienos viršūnės, statmenos priešingai pusei. Jie yra skirtingi trikampio taškai.
