• Kopimo į kalną algoritmas yra vietinis paieškos algoritmas, kuris nuolat juda aukščio / vertės didėjimo kryptimi, kad surastų kalno viršūnę arba geriausią problemos sprendimą. Jis baigiasi, kai pasiekia didžiausią vertę, kai joks kaimynas neturi didesnės vertės.
• Kopimo į kalną algoritmas yra metodas, naudojamas optimizuoti matematines problemas. Vienas iš plačiai aptartų kopimo į kalną algoritmo pavyzdžių yra „Traveling-salesman Problem“, kai turime sumažinti pardavėjo nuvažiuojamą atstumą.
• Ji taip pat vadinama gobšia vietine paieška, nes ji žiūri tik į gerą artimiausią kaimynę, o ne toliau.
• Kopimo į kalną algoritmo mazgas turi du komponentus: būseną ir vertę.
• Kopimas į kalną dažniausiai naudojamas, kai yra gera euristika.
• Taikant šį algoritmą, mums nereikia prižiūrėti ir tvarkyti paieškos medžio ar grafiko, nes jis išlaiko tik vieną dabartinę būseną.

Kopimo į kalną savybės:

Toliau pateikiamos kelios pagrindinės kopimo į kalną algoritmo ypatybės:

Sukurti ir išbandyti variantą:Kopimas į kalną yra generavimo ir bandymo metodo variantas. Generavimo ir testavimo metodas sukuria grįžtamąjį ryšį, kuris padeda nuspręsti, kuria kryptimi judėti paieškos erdvėje.Godus požiūris:Kopimo į kalną algoritmo paieška juda ta kryptimi, kuri optimizuoja išlaidas.Jokio atsitraukimo:Jis neatšaukia paieškos erdvės, nes neprisimena ankstesnių būsenų.

Laipiojimo į kalną būsenos erdvės diagrama:

Būsenos-erdvės peizažas yra grafinis kopimo į kalną algoritmo vaizdas, rodantis grafiką tarp įvairių algoritmo būsenų ir tikslo funkcijos / kainos.

eilučių masyvas c kalba

Y ašyje pasirinkome funkciją, kuri gali būti tikslo arba sąnaudų funkcija, o x ašyje – būsenos erdvę. Jei Y ašies funkcija yra kaina, paieškos tikslas yra rasti visuotinį minimumą ir vietinį minimumą. Jei Y ašies funkcija yra Objektyvi funkcija, tada paieškos tikslas yra rasti globalų maksimumą ir vietinį maksimumą.

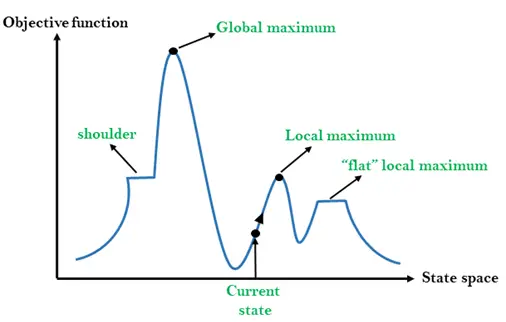
Įvairūs regionai valstybinės erdvės kraštovaizdyje:

Vietinis maksimalus: Vietinis maksimumas yra būsena, kuri yra geresnė už kaimynines valstybes, tačiau yra ir kita būsena, aukštesnė už ją.

Pasaulinis maksimalus: Globalus maksimumas yra geriausia įmanoma valstybės erdvės kraštovaizdžio būklė. Ji turi didžiausią tikslinės funkcijos reikšmę.

Dabartinė būsena: Tai kraštovaizdžio diagramos būsena, kurioje šiuo metu yra agentas.

kaip pervardyti katalogą linux

Maksimalus plotas: Tai plokščia kraštovaizdžio erdvė, kurioje visos kaimyninės dabartinių valstybių valstybės turi vienodą vertę.

Petys: Tai plokščiakalnio regionas, turintis įkalnę.

Kopimo į kalną algoritmų tipai:

• Paprastas kopimas į kalną:
• Stačiausias įkopimas į kalną:
• Stochastinis kopimas į kalną:

1. Paprastas kopimas į kalną:

Paprastas kopimas į kalną yra paprasčiausias būdas įgyvendinti kopimo į kalną algoritmą. Vienu metu jis įvertina tik kaimyninio mazgo būseną ir pasirenka pirmąjį, kuris optimizuoja dabartines išlaidas ir nustato ją kaip dabartinę būseną. . Jis tik patikrina, ar tai viena būsena, kurią pakeis, ir, jei ji randa geresnę už dabartinę būseną, tada perkelkite kitą būseną. Šis algoritmas turi šias funkcijas:

• Mažiau laiko
• Mažiau optimalus sprendimas ir sprendimas nėra garantuotas

Paprasto kopimo į kalną algoritmas:

1 žingsnis:Įvertinkite pradinę būseną, jei tai tikslo būsena, grąžinkite sėkmę ir sustokite.2 žingsnis:Ciklas, kol bus rastas sprendimas arba neliks naujo operatoriaus, kuriam būtų galima taikyti.3 veiksmas:Pasirinkite ir pritaikykite operatorių esamai būsenai.4 veiksmas:Patikrinkite naują būseną:
1. Jei tai tikslo būsena, grąžinkite sėkmę ir meskite.
2. Priešingu atveju, jei ji yra geresnė nei dabartinė, priskirkite naują būseną kaip dabartinę būseną.
3. Jei ne geresnė nei dabartinė būsena, grįžkite į 2 veiksmą.
5 veiksmas:Išeiti.

2. Kopimas į stačiausią įkalnę:

Stačiausio pakilimo algoritmas yra paprasto kopimo į kalną algoritmo variantas. Šis algoritmas tiria visus gretimus esamos būsenos mazgus ir parenka vieną kaimyninį mazgą, kuris yra arčiausiai tikslo būsenos. Šis algoritmas sunaudoja daugiau laiko, kai ieško kelių kaimynų

Įkopimo į stačiausią įkalnę algoritmas:

1 žingsnis:Įvertinkite pradinę būseną, jei tai tikslo būsena, grąžinkite sėkmę ir sustokite, kitu atveju nustatykite dabartinę būseną kaip pradinę būseną.2 žingsnis:Pakartokite, kol bus rastas sprendimas arba dabartinė būsena nepasikeis.
1. Tegul SUCC yra tokia būsena, kad bet kuris dabartinės būsenos įpėdinis bus geresnis už ją.
2. Kiekvienam operatoriui, kuris taikomas dabartinei būsenai:
   1. Taikykite naują operatorių ir sugeneruokite naują būseną.
   2. Įvertinkite naują būseną.
   3. Jei tai tikslo būsena, grąžinkite ją ir išeikite, kitaip palyginkite su SUCC.
   4. Jei ji yra geresnė nei SUCC, nustatykite naują būseną kaip SUCC.
   5. Jei SUCC yra geresnė už dabartinę būseną, nustatykite dabartinę būseną į SUCC.
5 veiksmas:Išeiti.

3. Stochastinis kopimas į kalną:

Stochastinis kopimas į kalną neištiria visų savo kaimynų prieš pajudėdamas. Atvirkščiai, šis paieškos algoritmas atsitiktinai parenka vieną kaimyninį mazgą ir nusprendžia, ar pasirinkti jį kaip esamą būseną, ar ištirti kitą būseną.

žemėlapio java iteratorius

Kopimo į kalną algoritmo problemos:

1. Vietinis maksimalus: Vietinis maksimumas yra didžiausia kraštovaizdžio būsena, kuri yra geresnė už kiekvieną kaimyninę būseną, tačiau yra ir kita būsena, kuri yra aukštesnė už vietinį maksimumą.

Sprendimas: Atbulinės eigos technika gali būti vietinio maksimumo sprendimas valstybinės erdvės kraštovaizdyje. Sukurkite perspektyvaus kelio sąrašą, kad algoritmas galėtų grįžti į paieškos erdvę ir ištirti kitus kelius.

mysql skaičius

2. Plokščiakalnis: Plokštuma yra plokščia paieškos erdvės sritis, kurioje visos kaimyninės esamos būsenos būsenos turi tą pačią reikšmę, nes šis algoritmas neranda jokios geriausios krypties judėti. Kopimo į kalną paieška gali būti prarasta plokščiakalnio srityje.

Sprendimas: Plokštumos sprendimas yra žengti didelius žingsnius arba labai mažais žingsneliais ieškant, išspręsti problemą. Atsitiktinai pasirinkite būseną, kuri yra toli nuo dabartinės būsenos, todėl gali būti, kad algoritmas gali rasti ne plokščiakalnio sritį.

3. Keteros: Kraigas yra ypatinga vietinio maksimumo forma. Jo plotas yra aukštesnis nei aplinkiniai, tačiau jis turi nuolydį ir negali būti pasiektas vienu judesiu.

Sprendimas: Naudodami dvikryptę paiešką arba judėdami skirtingomis kryptimis, galime išspręsti šią problemą.

Imituotas atkaitinimas:

Laipiojimo į kalną algoritmas, kuris niekada neperžengia mažesnės vertės, bus neišsamus, nes gali įstrigti ties vietiniu maksimumu. Ir jei algoritmas taiko atsitiktinį žingsnį, perkeldamas įpėdinį, jis gali būti baigtas, bet neveiksmingas. Imituotas atkaitinimas yra algoritmas, kuris užtikrina efektyvumą ir išsamumą.

Mechaniniu požiūriu Atkaitinimas yra metalo ar stiklo grūdinimo iki aukštos temperatūros ir palaipsniui aušinimo procesas, todėl metalas pasiekia mažos energijos kristalinę būseną. Tas pats procesas naudojamas imituojant atkaitinimą, kai algoritmas pasirenka atsitiktinį judesį, o ne geriausią judesį. Jei atsitiktinis judėjimas pagerina būseną, tada jis eina tuo pačiu keliu. Kitu atveju algoritmas eina keliu, kurio tikimybė mažesnė nei 1, arba juda žemyn ir pasirenka kitą kelią.