Regresijos ir tikimybinės klasifikacijos problemas galima išspręsti naudojant Gauso procesą (GP), prižiūrimą mokymosi techniką. Kadangi kiekvienas Gauso procesas gali būti suvokiamas kaip begalinis daugiamatis apibendrinimas Gauso skirstiniai , pavadinime yra terminas Gaussian. Šiame pranešime aptarsime Gauso proceso regresijos procesus, kurie taip pat vadinami Gauso proceso regresija (GPR). Daugybė realaus pasaulio problemų medžiagų mokslo, chemijos, fizikos ir biologijos srityse buvo išspręsta naudojant GPR.
Turinys
- Gauso proceso regresija (GPR)
- Pagrindinės Gauso proceso regresijos (GPR) sąvokos
- Matematinė Gauso proceso regresijos (GPR) samprata
- Gauso proceso įgyvendinimas Python
Gauso proceso regresija (GPR)
Gauso proceso regresija (GPR) yra galingas ir lankstus neparametrinės regresijos metodas, naudojamas mašininis mokymasis ir statistika . Tai ypač naudinga sprendžiant problemas, susijusias su nuolatiniais duomenimis, kai ryšys tarp įvesties kintamųjų ir išvesties nėra aiškiai žinomas arba gali būti sudėtingas. GPR yra Bajeso metodas, galintis modeliuoti prognozių tikrumą, todėl jis yra vertingas įrankis įvairioms programoms, įskaitant optimizavimą, laiko eilučių prognozavimą ir kt. GPR yra pagrįsta Gauso proceso koncepcija, kuri yra atsitiktinių dydžių rinkinys, kurių bet kuris baigtinis skaičius turi bendrą Gauso skirstinį. Gauso procesas gali būti laikomas funkcijų pasiskirstymu.
Pagrindinės Gauso proceso regresijos (GPR) sąvokos
Gaussaino procesas
Neparametrinis, tikimybinis modelis, vadinamas a Gauso procesas (GP) naudojamas statistikoje ir mašininiame mokyme regresijai, klasifikavimui ir neapibrėžtumo kiekybiniam įvertinimui. Jame pavaizduota atsitiktinių dydžių grupė, kurių kiekvienas turi bendrą Gauso skirstinį ir gali turėti baigtinį skaičių. GP yra universalus ir efektyvus būdas modeliuoti sudėtingus duomenų ryšius ir sudaryti prognozes su susijusiu neapibrėžtumu.
Gauso procesų charakteristikos :
- Neparametrinė prigimtis : GP gali prisitaikyti prie duomenų sudėtingumo, nes jie nepasikliauja nustatytu modelio parametrų skaičiumi
- Tikimybinės prognozės : bendrosios praktikos gydytojų prognozes galima įvertinti kiekybiškai, nes jie pateikia prognozes kaip tikimybių pasiskirstymą.
- Interpoliacija ir išlyginimas : GP yra naudingi esant triukšmingiems arba netaisyklingai atrinktiems duomenims, nes jie gerai išlygina triukšmingus duomenis ir interpoliuoja tarp duomenų taškų.
- Hiperparametrų marginalizavimas : panaikinus reikalavimą dėl aiškaus hiperparametrų koregavimo, jie pašalina hiperparametrus, todėl modelis tampa paprastesnis.
Vidutinė funkcija
Numatoma modeliuojamos funkcijos vertė kiekviename įvesties taške yra pavaizduota vidutinę funkciją Gauso procesuose (GP). Tai veikia kaip pagrindinė prielaida dėl pagrindinės duomenų struktūros. Vidutinė funkcija pagal numatytuosius nustatymus dažnai nustatoma į nulį, nebūtinai ir gali būti pakeista atsižvelgiant į duomenų ypatybes arba domeno patirtį. Darydamas įtaką pagrindinei prognozių tendencijai, jis padeda bendrosios praktikos gydytojams nustatyti duomenų modelius ar tendencijas. Šeimos gydytojai pateikia tikimybines prognozes, kuriose yra neapibrėžtumo, taip pat taškų įvertinimus, įtraukdami vidutinę funkciją
Kovariacijos (branduolio) funkcija
The kovariacijos funkcija , dar vadinama branduolio funkcija, matuoja, kiek įvesties duomenų taškai yra panašūs vienas į kitą Gauso procesuose (GP). Tai būtina charakterizuojant GP modelio elgesį, turintį įtakos funkcijų atrankai iš ankstesnio skirstinio. Kovariacijos funkcija matuoja porinius panašumus, kad būtų galima nustatyti koreliaciją tarp funkcijų verčių. GP gali prisitaikyti prie įvairių duomenų modelių, nuo sklandžių tendencijų iki sudėtingų struktūrų, nes skirtingos branduolio funkcijos fiksuoja skirtingas koreliacijas. Branduolio pasirinkimas gali turėti didelės įtakos modelio veikimui.
10 iš 50.00
Ankstesni platinimai
The išankstinis platinimas Gauso procesuose (GPs) yra mūsų funkcijų supratimas prieš stebint bet kokius duomenis. Paprastai jis apibūdinamas kovariacijos (branduolių) funkcija ir vidutine funkcija. Kovariacijos funkcija apibūdina funkcijų verčių panašumą arba koreliaciją įvairiuose įvesties taškuose, o vidutinė funkcija koduoja mūsų ankstesnius lūkesčius. Tai iš anksto naudoja bendrosios praktikos gydytojai, norėdami sukurti funkcijų paskirstymą. GP gali būti pasirenkami priorai, kurie atspindi duomenų neapibrėžtumą, integruoja srities žinias arba nurodo sklandumą.
Užpakaliniai pasiskirstymai
Gauso procesai vėlesnis platinimas rodomos mūsų peržiūrėtos prielaidos apie funkcijas po duomenų stebėjimo. Jis sujungia duomenų tikimybę, atsižvelgiant į funkciją ir ankstesnį pasiskirstymą. GP regresijos posterioras siūlo pasiskirstymą pagal funkcijas, kurios labiausiai atitinka stebimus duomenis. Leidžiant tikimybines prognozes ir kiekybiškai įvertinti neapibrėžtumą, užpakalinis pasiskirstymas atspindi kompromisą tarp ankstesnių įsitikinimų, saugomų ankstesniame paskirstyme, ir duomenų pateiktos informacijos.
Matematinė Gauso proceso regresijos (GPR) samprata
Regresijos užduotims atlikti naudojamas neparametrinis, tikimybinis mašininio mokymosi modelis, vadinamas Gauso proceso (GP) regresija. Modeliuojant sudėtingą ir dviprasmišką įvesties ir išvesties kintamųjų sąveiką, tai yra galingas įrankis. Manoma, kad daugiamatis Gauso skirstinys sukuria duomenų taškus GP regresijoje, o tikslas yra padaryti išvadą apie šį skirstinį.
GP regresijos modelis turi tokią matematinę išraišką. Tarkime, x1, x2,…..,xnyra įvesties duomenų taškai , kur x priklauso realiems skaičiams (-2,-1,0,1…), (xi
Tarkime, y1, ir2 ,……., irnyra išvesties reikšmės, kur yipriklauso realiajam skaičiui (yi
GP regresijos modelis daro prielaidą, kad Gauso procesas su vidutine funkcija (
Tada bandymo vietų x* rinkinyje f pasiskirstymas pateikiamas taip:
Paprastai branduolio funkcijos naudojamos vidutinei funkcijai ir kovariacijos funkcijai apibrėžti. Pavyzdžiui, dažnai naudojamas eksponentinis branduolys kvadratu apibūdinamas taip:
kur,
k(x_{i}, x_{j}) = Tai pavaizduota branduolio funkcija ir ji apskaičiuoja dviejų įvesties duomenų taškų koreliaciją arba panašumą, xiir xj.sigma^2 = Branduolio dispersijos parametras yra toks. Jis nustato branduolio funkcijos mastelį arba vertikalią sklaidą. Jis reguliuoja, kaip stipriai koreliuoja duomenų taškai. A aukštesnėsigma^2 duoda branduolio funkciją su didesne dispersija.- exp: Eksponentinė funkcija yra atsakinga už e padidinimą iki argumento galios.
||x_{i} – x_{j}||^2 : skirtumas tarp įvesties duomenų taškų, xiir xj, yra Euklido atstumas kvadratu. Matuojamas geometrinis atskyrimas tarp taškų objekto erdvėje.- l2: Tai yra branduolio ilgio skalės arba būdingo ilgio vaizdas. Jis reguliuoja branduolio funkcijos pablogėjimo greitį, kai duomenų taškai yra toliau vienas nuo kito. Mažesnis l sukelia branduolio degradaciją greičiau.
GP regresijos modelis taiko Bajeso išvadą, kad nustatytų f pasiskirstymą, kuris greičiausiai sukūrė duomenis, atsižvelgiant į mokymo duomenų rinkinį (x, y). Norint tai padaryti, turi būti apskaičiuotas užpakalinis f skirstinys, esantis duotais duomenimis, kuris apibrėžiamas taip:
kur ribinė duomenų tikimybė yra p(y|x), išankstinis f skirstinys yra p(f), o duomenų tikimybė, pateikta funkcijai f, yra (y|x,f).
Sužinojęs užpakalinį f pasiskirstymą, modelis apskaičiuoja užpakalinį nuspėjamąjį pasiskirstymą, kad padarytų prognozes papildomuose bandymo taškuose x*. Jį galima apibrėžti taip:
kaip java paversti eilutę į int
kur,
p(f^*|x*, y, x) = Tai rodo, atsižvelgiant į mokymo duomenis y ir x, sąlyginę numatomų funkcijos reikšmių f tikimybę*naujame įvesties taške x*Kitaip tariant, tai yra tikimybės pasiskirstymas per visas galimas funkcijos reikšmes naujoje įvesties vietoje x*, sąlygojama stebimų duomenų y ir jų atitinkančių įvesties vietų x.int p(f^*|x^*, f)p(f|y,x)df = Sąlyginei tikimybei nustatyti šioje lygties dalyje naudojamas integralas. Integralas apima visas potencialias funkcijos f reikšmes.p(f^*|x^*, f) = Tai numatomų funkcijos reikšmių f sąlyginis tikimybių skirstinys*ties x*, atsižvelgiant į funkcijos reikšmes f kai kuriose tarpinėse vietose.p(f|y,x) = Atsižvelgiant į stebimus duomenis (y) ir jų įvesties vietas (x), tai yra funkcijos reikšmių (f) sąlyginis tikimybių skirstinys.
Atliekant tokias užduotis kaip neapibrėžtumo suvokimo sprendimų priėmimas ir aktyvus mokymasis, šis paskirstymas siūlo prognozės neapibrėžtumo matą, kuris gali būti naudingas.
Gauso proceso regresijos žingsniai
- Duomenų rinkimas : surinkite įvesties ir išvesties duomenų poras savo regresijos problemai.
- Pasirinkite branduolio funkciją : pasirinkite tinkamą kovariacijos funkciją (brandulį), atitinkančią jūsų problemą. Branduolio pasirinkimas turi įtakos funkcijų, kurias gali modeliuoti GPR, formai.
- Parametrų optimizavimas : įvertinkite branduolio funkcijos hiperparametrus, padidindami duomenų tikimybę. Tai galima padaryti naudojant optimizavimo metodus, pvz., gradiento nusileidimą.
- Numatymas: Atsižvelgdami į naują įvestį, naudokite parengtą GPR modelį prognozėms. GPR pateikia ir numatomą vidurkį, ir susijusią neapibrėžtį (dispersiją).
Gauso proceso regresijos (GPR) įgyvendinimas
Python import numpy as np import matplotlib.pyplot as plt from sklearn.gaussian_process import GaussianProcessRegressor from sklearn.gaussian_process.kernels import RBF from sklearn.model_selection import train_test_split # Generate sample data np.random.seed(0) X = np.sort(5 * np.random.rand(80, 1), axis=0) y = np.sin(X).ravel() # Add noise to the data y += 0.1 * np.random.randn(80) # Define the kernel (RBF kernel) kernel = 1.0 * RBF(length_scale=1.0) # Create a Gaussian Process Regressor with the defined kernel gp = GaussianProcessRegressor(kernel=kernel, n_restarts_optimizer=10) # Split the data into training and testing sets X_train, X_test, y_train, y_test = train_test_split( X, y, test_size=0.5, random_state=0) # Fit the Gaussian Process model to the training data gp.fit(X_train, y_train) # Make predictions on the test data y_pred, sigma = gp.predict(X_test, return_std=True) # Visualize the results x = np.linspace(0, 5, 1000)[:, np.newaxis] y_mean, y_cov = gp.predict(x, return_cov=True) plt.figure(figsize=(10, 5)) plt.scatter(X_train, y_train, c='r', label='Training Data') plt.plot(x, y_mean, 'k', lw=2, zorder=9, label='Predicted Mean') plt.fill_between(x[:, 0], y_mean - 1.96 * np.sqrt(np.diag(y_cov)), y_mean + 1.96 * np.sqrt(np.diag(y_cov)), alpha=0.2, color='k', label='95% Confidence Interval') plt.xlabel('X') plt.ylabel('y') plt.legend() plt.show()> Išvestis:
Šiame kode pirmiausia sugeneruokite keletą pavyzdinių duomenų taškų su pridėtiniu triukšmu, tada apibrėžkite RBF branduolį ir sukurkite a Gauso proceso regresorius su tuo. Modelis yra apmokytas pagal mokymo duomenis ir naudojamas prognozuoti bandymo duomenis. Galiausiai rezultatai vizualizuojami naudojant diagramą, kurioje rodomi treniruočių duomenys, numatomas vidurkis ir 95% pasikliautinasis intervalas.
Gauso proceso įgyvendinimas Python
Scikit Sužinokite
Python import matplotlib.pyplot as plt import numpy as np from scipy import linalg from sklearn.gaussian_process import kernels,GaussianProcessRegressor ## check version import sys import sklearn print(sys.version) !python --version print("numpy:", np.__version__) print("sklearn:",sklearn.__version__)> Šiuo kodu importuojamos būtinos bibliotekos Gauso proceso regresijai (GPR) Python; Šitie yra SciPy tiesinėms algebros funkcijoms, NumPy skaitinėms operacijoms ir Matplotlib duomenų vizualizavimui. Kad įsitikintų, ar jis suderinamas su reikiamais paketais, jis papildomai patikrina Python versiją ir išspausdina ją kartu su NumPy ir scikit-learn (sklearn) versijomis.
Branduolio pasirinkimas
Python np.random.seed(0) n=50 kernel_ =[kernels.RBF (), kernels.RationalQuadratic(), kernels.ExpSineSquared(periodicity=10.0), kernels.DotProduct(sigma_0=1.0)**2, kernels.Matern() ] print(kernel_, '
')> Išvestis:
[RBF(ilgio_mastas=1),
RationalQuadratic (alfa=1, ilgio_mastas=1),
ExpSineSquared(ilgio_mastas=1, periodiškumas=10),
DotProduct(sigma_0=1)** 2,
Motinos (ilgio_mastas=1, nu=1,5)]
Kodas nurodo bandymo vietų skaičių (n) ir inicijuoja a atsitiktinė sėkla . Kad būtų rodomi pasirinkti branduoliai, jis sugeneruoja kelių branduolio funkcijų sąrašą ir išspausdina sąrašą.
Branduolio palyginimas ir vizualizacija
Python for kernel in kernel_: # Gaussian process gp = GaussianProcessRegressor(kernel=kernel) # Prior x_test = np.linspace(-5, 5, n).reshape(-1, 1) mu_prior, sd_prior = gp.predict(x_test, return_std=True) samples_prior = gp.sample_y(x_test, 3) # plot plt.figure(figsize=(10, 3)) plt.subplot(1, 2, 1) plt.plot(x_test, mu_prior) plt.fill_between(x_test.ravel(), mu_prior - sd_prior, mu_prior + sd_prior, color='aliceblue') plt.plot(x_test, samples_prior, '--') plt.title('Prior') # Fit x_train = np.array([-4, -3, -2, -1, 1]).reshape(-1, 1) y_train = np.sin(x_train) gp.fit(x_train, y_train) # posterior mu_post, sd_post = gp.predict(x_test, return_std=True) mu_post = mu_post.reshape(-1) samples_post = np.squeeze(gp.sample_y(x_test, 3)) # plot plt.subplot(1, 2, 2) plt.plot(x_test, mu_post) plt.fill_between(x_test.ravel(), mu_post - sd_post, mu_post + sd_post, color='aliceblue') plt.plot(x_test, samples_post, '--') plt.scatter(x_train, y_train, c='blue', s=50) plt.title('Posterior') plt.show() print("gp.kernel_", gp.kernel_) print("gp.log_marginal_likelihood:", gp.log_marginal_likelihood(gp.kernel_.theta)) print('-'*50, '
')> Išvestis:
RBF
gp.kernel_ RBF(ilgio_mastas=1,93)
gp.log_marginal_likelihood: -3.444937833462133
--------------------------------------------------- -
Diana Ankudinova
Racionalus kvadratinis

gp.kernel_ RationalQuadratic(alpha=1e+05, long_scale=1.93)
gp.log_marginal_likelihood: -3.4449718909150966
---------------------------------------------------
ExpSineSquared

gp.kernel_ ExpSineSquared(ilgio_mastas=0,000524, periodiškumas=2,31e+04)
gp.log_marginal_likelihood: -3.4449381454930217
---------------------------------------------------
Taškinis produktas

gp.kernel_ DotProduct(sigma_0=0,998)** 2
gp.log_marginal_likelihood: -150204291.56018084
---------------------------------------------------
Motinos

gp.kernel_ Matern(ilgio_mastas=1,99, nu=1,5)
gp.log_marginal_likelihood: -5.131637070524745
---------------------------------------------------
Kodas pradedamas perjungiant įvairias branduolio funkcijas, išvardytas kernel_ sąraše. Gauso proceso regresorius (gp) sukuriamas naudojant konkretų kiekvieno branduolio branduolį. Gauso procesui tai nustato kovariacijos struktūrą. Norint įvertinti ankstesnį pasiskirstymą, nustatomas testo įvesties taškų rinkinys, vadinamas x_test, kurio reikšmės svyruoja nuo -5 iki 5. Ši taškų rinkinys paverčiamas stulpelio vektoriumi.
Naudojant gp.predict metodą, kiekviename bandymo taške nustatomas išankstinio skirstinio vidurkis (mu_prior) ir standartinis nuokrypis (sd_prior). Standartinio nuokrypio verčių prašoma naudojant parinktį return_std=True. gp.sample_y (x_test, 3) naudojamas norint gauti tris funkcijų pavyzdžius iš ankstesnio paskirstymo.
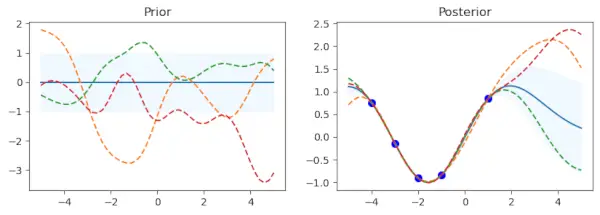
Pirmajame diagramoje rodomas ankstesnio pasiskirstymo vidurkis, o standartinis nuokrypis rodomas tamsesniu plotu. Mėginiai yra išdėstyti kaip punktyrinės linijos, o vidurkis rodomas kaip ištisinė linija. Yra dalinis sklypas, vadinamas „Prior“. Yra apibrėžtas mokymo duomenų taškų rinkinys (x_train) ir tikslo reikšmės (y_train), kurios yra su jais susijusios. Gauso proceso modelis pritaikytas naudojant šiuos taškus (gp.fit(x_train, y_train)). Penki duomenų taškai su atitinkamomis sinusinėmis reikšmėmis sudaro treniruočių duomenis šiame kode.
oi sąvokos
Po mokymo duomenų derinimo etapo procedūra apskaičiuoja užpakalinio pasiskirstymo vidurkį (mu_post) ir standartinį nuokrypį (sd_post) tiems patiems bandymo taškams (x_test). gp.sample_y(x_test, 3) taip pat naudojamas funkcijų pavyzdžiams iš užpakalinio skirstinio sukurti. Antrasis brėžinys perdengia atrinktas funkcijas kaip punktyrines linijas ir rodo užpakalinio pasiskirstymo vidurkį, nuspalvintą standartiniu nuokrypiu. Mėlyna spalva pavaizduoti treniruočių duomenų taškai. Subsiužetas turi pavadinimą Posterior.
Norėdami pamatyti ankstesnius ir užpakalinius dabartinio branduolio brėžinius ir vizualiai suprasti modelio veikimą, iškvieskite Matplotlib funkciją plt.show().
Kodas rodo išsamią informaciją apie esamą branduolį, pvz., gp.kernel_, kuris nurodo dabartinį naudojamą branduolį ir gp.log_marginal_likelihood (gp.kernel_.theta), kuri suteikia modelio, naudojančio dabartinį branduolį, ribinę tikimybę po kiekvieno ankstesnių ir užpakalinių brėžinių rinkinio.
Gauso proceso regresijos (GPR) pranašumai
Gauso proceso regresija (GPR) turi daug privalumų įvairiose srityse:
- GPR pateikia tikimybinę regresijos sistemą, o tai reiškia, kad ji ne tik pateikia taškinius įverčius, bet ir prognozių neapibrėžtumo įverčius.
- Jis yra labai lankstus ir gali užfiksuoti sudėtingus duomenų ryšius.
- GPR gali būti pritaikytas įvairioms programoms, įskaitant laiko eilučių prognozavimą, optimizavimą ir Bajeso optimizavimą.
Gauso proceso regresijos (GPR) iššūkiai
- GPR gali būti brangus skaičiavimais dirbant su dideliais duomenų rinkiniais, nes reikalinga kovariacijos matricos inversija.
- Branduolio funkcijos ir jos hiperparametrų pasirinkimas gali labai paveikti modelio veikimą.
Geri GPR programų pavyzdžiai
- Akcijų kainos prognozė: GPR gali būti naudojamas akcijų kainoms modeliuoti ir prognozuoti, atsižvelgiant į finansų rinkų nepastovumą ir neapibrėžtumą.
- Kompiuteriniai eksperimentai: GPR yra naudingas optimizuojant sudėtingus modeliavimus, modeliuojant įvesties ir išvesties ryšius ir nustatant įtakingiausius parametrus.
- Anomalijų aptikimas: GPR gali būti taikomas anomalijų aptikimui, kai jis nustato neįprastus laiko eilučių duomenų modelius, fiksuodamas įprastą duomenų pasiskirstymą.
Išvada
Apibendrinant galima pasakyti, kad Gauso proceso regresija yra vertinga priemonė duomenų analizei ir prognozavimui situacijose, kai būtina suprasti prognozių neapibrėžtumą. Naudodamas tikimybinį modeliavimą ir branduolio funkcijas, GPR gali pateikti tikslius ir interpretuojamus rezultatus. Tačiau, įgyvendinant GPR praktikoje, labai svarbu atsižvelgti į skaičiavimo išlaidas ir ekspertų indėlio poreikį.
