Ford-Fulkerson algoritmas yra plačiai naudojamas algoritmas siekiant išspręsti didžiausio srauto problemą srauto tinkle. Didžiausio srauto problema apima didžiausio srauto kiekio, kuris gali būti siunčiamas iš šaltinio viršūnės į kriauklės viršūnę nukreiptame svertiniame grafike, nustatymą, atsižvelgiant į talpos apribojimus kraštuose.

Algoritmas veikia iteratyviai surandant padidinimo kelią, kuris yra kelias nuo šaltinio iki kriauklės likutiniame grafike, ty grafikas, gautas atėmus srovės srautą iš kiekvienos briaunos talpos. Tada algoritmas padidina srautą šiuo keliu maksimaliu įmanomu dydžiu, kuris yra mažiausia pakraščių išilgai kelio talpa.

javascript data

Problema:

Pateiktas grafikas, vaizduojantis srauto tinklą, kuriame kiekvienas kraštas turi talpą. Be to, atsižvelgiant į dvi viršūnes šaltinis 'smėlis kriauklė „t“ grafike raskite didžiausią galimą srautą nuo s iki t su šiais apribojimais:

• Srautas briaunoje neviršija nurodytos krašto talpos.
• Įeinantis srautas yra lygus išeinančiam srautui kiekvienoje viršūnėje, išskyrus s ir t.

Pavyzdžiui, apsvarstykite šią grafiką iš CLRS knygos.

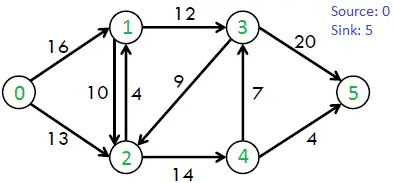
Didžiausias galimas srautas aukščiau pateiktoje diagramoje yra 23.

Būtina sąlyga: Didžiausio srauto problemos įvadas

Fordo-Fulkersono algoritmas

Toliau pateikiama paprasta Ford-Fulkerson algoritmo idėja:

1. Pradėkite nuo pradinio srauto kaip 0.
2. Nors yra papildantis kelias nuo šaltinio iki kriauklės:
   • Raskite padidinimo kelią naudodami bet kokį kelio paieškos algoritmą, pvz., paiešką pagal plotį arba paiešką pagal gylį.
   • Nustatykite srauto kiekį, kuris gali būti siunčiamas didinimo keliu, kuris yra mažiausia liekamoji talpa išilgai kelio kraštų.
   • Nustatytu kiekiu padidinkite srautą didinimo keliu.
3. Grąžinkite maksimalų srautą.

Laiko sudėtingumas: Aukščiau pateikto algoritmo laiko sudėtingumas yra O(max_flow * E). Vykdome kilpą, kol yra didinimo kelias. Blogiausiu atveju kiekvienoje iteracijoje galime pridėti 1 srauto vienetą. Todėl laiko sudėtingumas tampa O(max_flow * E).

Kaip įgyvendinti aukščiau pateiktą paprastą algoritmą?
Pirmiausia apibrėžkime likutinio grafiko sąvoką, kurios reikia norint suprasti įgyvendinimą.

Likutinis grafikas srauto tinklo grafikas, rodantis papildomą galimą srautą. Jei liekaniniame grafike yra kelias nuo šaltinio iki grimzlės, tada galima pridėti srautą. Kiekviena liekamojo grafiko briauna turi reikšmę, vadinamą likutinė talpa kuri yra lygi pradinei krašto galiai atėmus srovės srautą. Liekamoji talpa iš esmės yra dabartinė krašto talpa.

Dabar pakalbėkime apie įgyvendinimo detales. Liekamoji talpa yra 0, jei tarp dviejų liekamojo grafo viršūnių nėra briaunos. Likutinį grafiką galime inicijuoti kaip pradinį grafiką, nes nėra pradinio srauto ir iš pradžių likutinė talpa yra lygi pradinei talpai. Norėdami rasti padidinimo kelią, galime atlikti likusio grafiko BFS arba DFS. Mes naudojome BFS toliau pateiktame įgyvendinime. Naudodami BFS galime sužinoti, ar yra kelias nuo šaltinio iki kriauklės. BFS taip pat sukuria pirminį [] masyvą. Naudodami pirminį [] masyvą, pereiname rastu keliu ir surandame galimą srautą šiuo keliu, surasdami mažiausią liekamąją talpą kelyje. Vėliau rastą kelio srautą pridedame prie bendro srauto.

Svarbu tai, kad turime atnaujinti likutinius grafiko likučius. Iš visų kelio kraštų atimame kelio srautą ir pridedame kelio srautą išilgai atvirkštinių kraštų Turime pridėti kelio srautą išilgai priešingų kraštų, nes vėliau gali tekti siųsti srautą atvirkštine kryptimi (žr. toliau pateiktą nuorodą).

Žemiau pateikiamas Ford-Fulkerson algoritmo įgyvendinimas. Kad viskas būtų paprasta, grafikas vaizduojamas kaip 2D matrica.

C++

>

>

Java

btree ir b medis

> 
    
   
 
     
  
 
    
 
     
     
    
 
 
 
 
 
 # Python program for implementation> # of Ford Fulkerson algorithm> from> collections>import> defaultdict> # This class represents a directed graph> # using adjacency matrix representation> class> Graph:> >def> __init__(>self>, graph):> >self>.graph>=> graph># residual graph> >self>. ROW>=> len>(graph)> ># self.COL = len(gr[0])> >'''Returns true if there is a path from source 's' to sink 't' in> >residual graph. Also fills parent[] to store the path '''> >def> BFS(>self>, s, t, parent):> ># Mark all the vertices as not visited> >visited>=> [>False>]>*>(>self>.ROW)> ># Create a queue for BFS> >queue>=> []> ># Mark the source node as visited and enqueue it> >queue.append(s)> >visited[s]>=> True> ># Standard BFS Loop> >while> queue:> ># Dequeue a vertex from queue and print it> >u>=> queue.pop(>0>)> ># Get all adjacent vertices of the dequeued vertex u> ># If a adjacent has not been visited, then mark it> ># visited and enqueue it> >for> ind, val>in> enumerate>(>self>.graph[u]):> >if> visited[ind]>=>=> False> and> val>>>:> ># If we find a connection to the sink node,> ># then there is no point in BFS anymore> ># We just have to set its parent and can return true> >queue.append(ind)> >visited[ind]>=> True> >parent[ind]>=> u> >if> ind>=>=> t:> >return> True> ># We didn't reach sink in BFS starting> ># from source, so return false> >return> False> > > ># Returns the maximum flow from s to t in the given graph> >def> FordFulkerson(>self>, source, sink):> ># This array is filled by BFS and to store path> >parent>=> [>->1>]>*>(>self>.ROW)> >max_flow>=> 0> # There is no flow initially> ># Augment the flow while there is path from source to sink> >while> self>.BFS(source, sink, parent) :> ># Find minimum residual capacity of the edges along the> ># path filled by BFS. Or we can say find the maximum flow> ># through the path found.> >path_flow>=> float>(>'Inf'>)> >s>=> sink> >while>(s !>=> source):> >path_flow>=> min> (path_flow,>self>.graph[parent[s]][s])> >s>=> parent[s]> ># Add path flow to overall flow> >max_flow>+>=> path_flow> ># update residual capacities of the edges and reverse edges> ># along the path> >v>=> sink> >while>(v !>=> source):> >u>=> parent[v]> >self>.graph[u][v]>->=> path_flow> >self>.graph[v][u]>+>=> path_flow> >v>=> parent[v]> >return> max_flow> > # Create a graph given in the above diagram> graph>=> [[>0>,>16>,>13>,>0>,>0>,>0>],> >[>0>,>0>,>10>,>12>,>0>,>0>],> >[>0>,>4>,>0>,>0>,>14>,>0>],> >[>0>,>0>,>9>,>0>,>0>,>20>],> >[>0>,>0>,>0>,>7>,>0>,>4>],> >[>0>,>0>,>0>,>0>,>0>,>0>]]> g>=> Graph(graph)> source>=> 0>; sink>=> 5> > print> (>'The maximum possible flow is %d '> %> g.FordFulkerson(source, sink))> # This code is contributed by Neelam Yadav> 
 
 
 
 
    
 
>
 
    
 
>
 
 
C#
    
 
     
  
 
    
bash if teiginys
 
     
     
    
 
 
 
 
 
 // C# program for implementation> // of Ford Fulkerson algorithm> using> System;> using> System.Collections.Generic;> public> class> MaxFlow {> >static> readonly> int> V = 6;>// Number of vertices in> >// graph> >/* Returns true if there is a path> >from source 's' to sink 't' in residual> >graph. Also fills parent[] to store the> >path */> >bool> bfs(>int>[, ] rGraph,>int> s,>int> t,>int>[] parent)> >{> >// Create a visited array and mark> >// all vertices as not visited> >bool>[] visited =>new> bool>[V];> >for> (>int> i = 0; i   visited[i] = false;  // Create a queue, enqueue source vertex and mark  // source vertex as visited  List eilė = naujas sąrašas ();  eilė. Pridėti(s);  aplankytas(iai) = tiesa;  tėvas (-iai) = -1;  // Standartinis BFS ciklas while (eilė.Skaičius != 0) { int u = eilė[0];  eilė.RemoveAt(0);  for (int v = 0; v if (aplankytas[v] == false && rGraph[u, v]> 0) { // Jei rasime ryšį su kriaukle // mazgu, tada BFS nėra prasmės / / nebe Mes tiesiog turime nustatyti jo pirminį // ir galime grąžinti true if (v == t) { parent[v] = u return true.Add(v) = u; v] = true } } } // Mes nepasiekėme sink BFS, pradedant nuo šaltinio, // taigi return false return false } // Grąžina maksimalų srautą // nuo s iki t duotame grafike int fordFulkerson; (int[, ] grafikas, int s, int t) { int u, v // Sukurkite likutinį grafiką ir užpildykite // likutinį grafiką duotomis // pradinio grafiko talpomis kaip // likutinės talpos grafike /; / Likutinis grafikas, kuriame rGrafas[i,j] // rodo // krašto likutinę talpą nuo i iki j (jei yra // briauna. Jei rGrafas[i,j] yra 0, tai // nėra) int [, ] rGrafas = naujas int[V, V] to store path int[] parent = new int[V];  int max_flow = 0; // Iš pradžių srauto nėra // Padidinkite srautą, kol yra kelias nuo šaltinio // iki nugrimzdimo, o (bfs(rGraph, s, t, pirminis)) { // Rasti mažiausią liekamąją kraštų talpą // palei kelią užpildytas BFS. Arba galime pasakyti // rasti maksimalų srautą per rastą kelią.  int kelias_srautas = int.MaxValue;  for (v = t; v != s; v = pirminis [v]) { u = pirminis [v];  kelias_srautas = Math.Min(kelio_srautas, rGrafas[u, v]);  } // Atnaujinti liekamąsias briaunų ir // atvirkštinių kraštų talpas palei kelią (v = t; v != s; v = pirminis[v]) { u = pirminis[v];  rGrafas[u, v] -= kelias_srautas;  rGrafas[v, u] += kelias_srauto;  } // Pridėti kelio srautą prie bendro srauto max_flow += path_flow;  } // Grąžina bendrą srautą return max_flow;  } // Tvarkyklės kodas public static void Main() { // Sukurkime grafiką, parodytą aukščiau pateiktame pavyzdyje int[, ] graph = new int[, ] { { 0, 16, 13, 0, 0, 0 }, { 0, 0, 10, 12, 0, 0 }, { 0, 4, 0, 0, 14, 0 }, { 0, 0, 9, 0, 0, 20 }, { 0, 0, 0, 7 , 0, 4 }, { 0, 0, 0, 0, 0, 0 } };  MaxFlow m = naujas MaxFlow();  Console.WriteLine('Didžiausias galimas srautas yra ' + m.fordFulkerson(graph, 0, 5));  } } /* Šį kodą pateikė PrinciRaj1992 */>
 
 
 
 
    
 
>
 
    
 
>
 
 
Javascript
    
 
     
  
 
    
 
     
     
    
 
 
 
 
 
 > // Javascript program for implementation of Ford> // Fulkerson algorithm> // Number of vertices in graph> let V = 6;> // Returns true if there is a path from source> // 's' to sink 't' in residual graph. Also> // fills parent[] to store the path> function> bfs(rGraph, s, t, parent)> {> > >// Create a visited array and mark all> >// vertices as not visited> >let visited =>new> Array(V);> >for>(let i = 0; i   visited[i] = false;  // Create a queue, enqueue source vertex  // and mark source vertex as visited  let queue = [];  queue.push(s);  visited[s] = true;  parent[s] = -1;  // Standard BFS Loop  while (queue.length != 0)  {  let u = queue.shift();  for(let v = 0; v   {  if (visited[v] == false &&   rGraph[u][v]>0) { // Jei rasime ryšį su kriaukle // mazgu, tada BFS // nebėra prasmės. Tiesiog turime nustatyti jo pirminį // ir galime grąžinti teisingą, jei (v == t) { tėvas[ v] = u;  grįžti tiesa;  } eilė.push(v);  tėvas [v] = u;  aplankytas[v] = tiesa;  } } } // Mes nepasiekėme sink BFS pradedant // nuo šaltinio, todėl return false return false; } // Grąžina maksimalų srautą nuo s iki t // duotoje grafo funkcijoje fordFulkerson(graph, s, t) { tegul u, v;    // Sukurkite likutinį grafiką ir užpildykite // likutinį grafiką nurodytomis talpomis // pradiniame grafike kaip likutinį // talpos likutiniame grafike // Likutinis grafikas, kur rGraph[i][j] // rodo likutinę briaunos talpą // / nuo i iki j (jei yra briauna. // Jei rGrafas[i][j] yra 0, tai yra // ne) tegul rGraph = new Array(V);  for(u = 0; u { rGrafas[u] = naujas masyvas(V); for(v = 0; v rGrafas[u][v] = grafikas[u][v]; } // Šis masyvas užpildytas BFS ir saugojimo kelias tegul tėvas = naujas Masyvas (V) // Iš pradžių nėra srauto, kad max_flow = 0 , pirminis)) { // Rasti minimalią kraštinių talpą // palei kelią, kurį užpildo BFS v != s; u = pirminis [v] atvirkštinės briaunos išilgai (v = t; v != s; v = pirminis[v]) { u = pirminis[v] - rGrafas[v][u] +; = path_flow } // Pridėti kelio srautą į bendrą srautą += kelias_srauto , 16, 13, 0, 0, 0], [0, 0, 10, 12, 0, 0], [0, 4, 0, 0, 14, 0], [0, 0, 9, 0, 0 , 20 ], [ 0, 0, 0, 7, 0, 4 ], [ 0, 0, 0, 0, 0, 0 ]]; document.write('Didžiausias galimas srautas yra ' + fordFulkerson(grafas, 0, 5)); // Šį kodą sukūrė avanitrachhadiya2155>>
 
 
 
 
    
 
> 
    
 The maximum possible flow is 23>
 
  Laiko sudėtingumas : O(|V| * E^2) ,kur E – briaunų skaičius, o V – viršūnių skaičius.
 
  Erdvės sudėtingumas: O(V), kaip mes sukūrėme eilę.
 
Aukščiau pateiktas Ford Fulkerson algoritmo įgyvendinimas vadinamas   Edmonds-Karp algoritmas   . Edmonds-Karp idėja yra naudoti BFS Ford Fulkerson diegime, nes BFS visada pasirenka kelią su minimaliu briaunų skaičiumi. Kai naudojamas BFS, blogiausio atvejo laiko sudėtingumas gali būti sumažintas iki O (VE2). Aukščiau pateiktame įgyvendinime naudojamas gretimų matricos vaizdas, nors BFS ima O (V2) laiko, aukščiau nurodyto įgyvendinimo laiko sudėtingumas yra O(EV3) (žr CLRS knyga laiko sudėtingumo įrodymui)
 
Tai svarbi problema, nes ji iškyla daugelyje praktinių situacijų. Pavyzdžiai: maksimalus transportavimas esant tam tikroms srauto riboms, maksimaliai padidintas paketų srautas kompiuterių tinkluose. 
Dinc algoritmas maksimaliam srautui.
 
  Pratimas:   
Pakeiskite aukščiau pateiktą įgyvendinimą, kad jis veiktų O(VE2) laikas.