The Floydo-Warshall algoritmas , pavadintas jo kūrėjų vardu Robertas Floydas ir Stephenas Warshallas , yra pagrindinis informatikos ir grafų teorijos algoritmas. Jis naudojamas norint rasti trumpiausius kelius tarp visų svertinio grafiko mazgų porų. Šis algoritmas yra labai efektyvus ir gali tvarkyti grafikus su abiem teigiamas ir n lyginamieji briaunos svoriai , todėl tai yra universalus įrankis įvairioms tinklo ir ryšio problemoms spręsti.
Turinys
- Floydo Warshall algoritmas
- Idėja už Floydo Warshall algoritmo
- Floydo Warshallo algoritmo algoritmas
- Floydo Warshallo algoritmo pseudokodas
- Floydo Warshallo algoritmo iliustracija
- Floydo Warshall algoritmo sudėtingumo analizė
- Kodėl Floydo-Warshall algoritmas tinka tankiems, o ne retiems grafikams?
- Svarbūs interviu klausimai, susiję su Floyd-Warshall
- Realaus pasaulio Floydo-Warshall algoritmo taikymas
Floydo Warshall algoritmas:
The Floydo Warshall algoritmas yra visų porų trumpiausio kelio algoritmas, kitaip nei Dijkstra ir Belmanas Fordas kurie yra vieno šaltinio trumpiausio kelio algoritmai. Šis algoritmas veikia tiek nukreiptas ir nenukreiptas svertinis grafikai. Tačiau tai neveikia grafikams su neigiamais ciklais (kai ciklo briaunų suma yra neigiama). Iš to seka Dinaminis programavimas metodas, skirtas patikrinti kiekvieną galimą kelią, einantį per visus galimus mazgus, siekiant apskaičiuoti trumpiausią atstumą tarp kiekvienos mazgų poros.
powershell komentaras kelių eilučių
Idėja už Floydo Warshall algoritmo:
Tarkime, kad turime grafiką G[][] su IN viršūnės iš 1 į N . Dabar turime įvertinti a shortestPathMatrix[][] kur yra hortestPathMatrix[i][j] reiškia trumpiausią kelią tarp viršūnių i ir j .
Akivaizdu, kad trumpiausias kelias tarp i į j turės keletą k tarpinių mazgų skaičius. Floyd Warshall algoritmo idėja yra apdoroti kiekvieną viršūnę 1 į N kaip tarpinis mazgas po vieną.
Toliau pateiktame paveikslėlyje parodyta aukščiau pateikta optimali substruktūros savybė floyd Warshall algoritme:
Floydo Warshall algoritmo algoritmas:
- Pirmiausia inicijuokite sprendimo matricą kaip ir įvesties grafiko matricą.
- Tada atnaujinkite sprendimo matricą, visas viršūnes laikydamos tarpine viršūne.
- Idėja yra pasirinkti visas viršūnes po vieną ir atnaujinti visus trumpiausius kelius, kurie apima pasirinktą viršūnę kaip tarpinę trumpiausio kelio viršūnę.
- Kai pasirenkame viršūnės skaičių k kaip tarpinę viršūnę, mes jau svarstėme viršūnes 0, 1, 2, .. k-1} kaip tarpines viršūnes.
- Kiekvienai porai (i, j) atitinkamai šaltinio ir paskirties viršūnių, yra du galimi atvejai.
- k nėra tarpinė viršūnė trumpiausiu keliu nuo i į j . Mes išlaikome vertę dist[i][j] taip kaip yra.
- k yra tarpinė viršūnė trumpiausiu keliu nuo i į j . Atnaujiname vertę dist[i][j] kaip dist[i][k] + dist[k][j], jeigu dist[i][j]> dist[i][k] + dist[k][j]
Floydo Warshall algoritmo pseudokodas:>
Kai k = 0 iki n – 1
Jei i = 0 iki n – 1
Jei j = 0 iki n – 1
Atstumas[i, j] = min(atstumas[i, j], atstumas[i, k] + atstumas[k, j])kur i = šaltinio mazgas, j = paskirties mazgas, k = tarpinis mazgas
Floydo Varšalo algoritmo iliustracija:
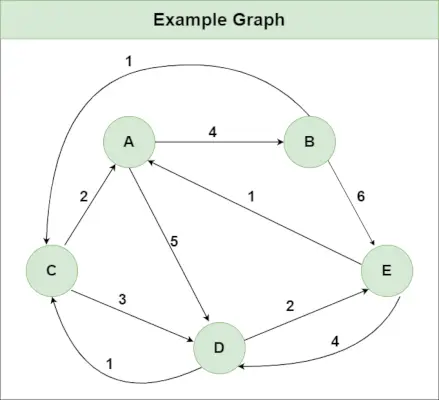
Rekomenduojama praktika Išbandykite!Tarkime, kad turime grafiką, kaip parodyta paveikslėlyje:
1 žingsnis : Naudodami įvesties grafiką inicijuokite atstumo[][] matricą taip, kad atstumas[i][j] = krašto svoris nuo i į j , taip pat Atstumas[i][j] = Begalybė, jei nėra briaunos nuo i į j.
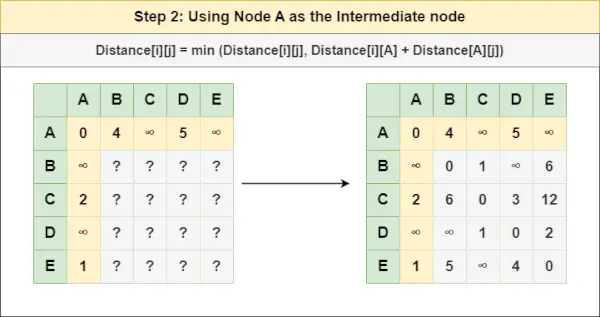
2 žingsnis : Gydymo mazgas A kaip tarpinį mazgą ir apskaičiuokite atstumą[][] kiekvienai {i,j} mazgų porai naudodami formulę:
python os listdir= atstumas[i][j] = mažiausias (atstumas[i][j], (atstumas nuo i iki A ) + (Atstumas nuo A į j))
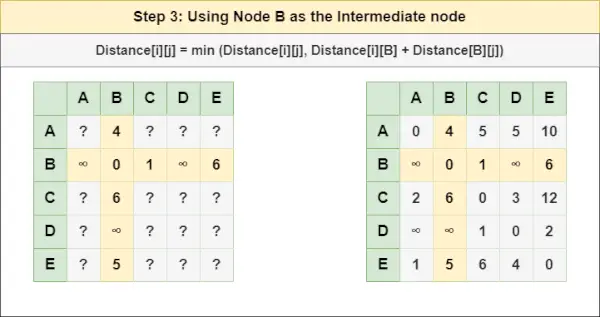
= atstumas[i][j] = mažiausias (atstumas[i][j], atstumas[i][ A ] + atstumas[ A ][j])3 veiksmas : Gydymo mazgas B kaip tarpinį mazgą ir apskaičiuokite atstumą[][] kiekvienai {i,j} mazgų porai naudodami formulę:
= atstumas[i][j] = mažiausias (atstumas[i][j], (atstumas nuo i iki B ) + (Atstumas nuo B į j))
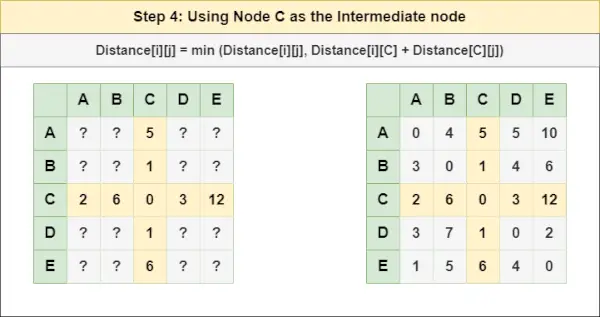
= atstumas[i][j] = mažiausias (atstumas[i][j], atstumas[i][ B ] + atstumas[ B ][j])4 veiksmas : Gydymo mazgas C kaip tarpinį mazgą ir apskaičiuokite atstumą[][] kiekvienai {i,j} mazgų porai naudodami formulę:
= atstumas[i][j] = mažiausias (atstumas[i][j], (atstumas nuo i iki C ) + (Atstumas nuo C į j))
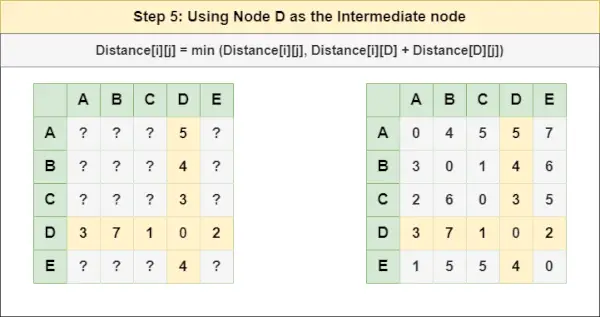
= atstumas[i][j] = mažiausias (atstumas[i][j], atstumas[i][ C ] + atstumas[ C ][j])5 veiksmas : Gydymo mazgas D kaip tarpinį mazgą ir apskaičiuokite atstumą[][] kiekvienai {i,j} mazgų porai naudodami formulę:
eilutę prie itn= atstumas[i][j] = mažiausias (atstumas[i][j], (atstumas nuo i iki D ) + (Atstumas nuo D į j))
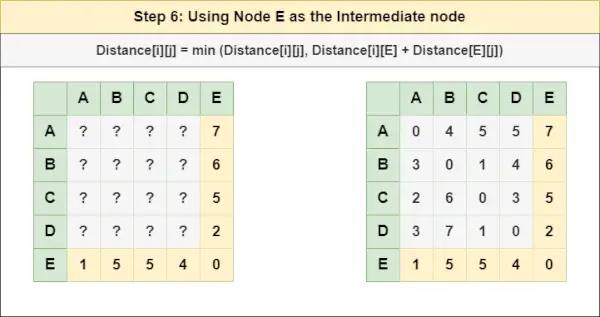
= atstumas[i][j] = mažiausias (atstumas[i][j], atstumas[i][ D ] + atstumas[ D ][j])6 veiksmas : Gydymo mazgas IR kaip tarpinį mazgą ir apskaičiuokite atstumą[][] kiekvienai {i,j} mazgų porai naudodami formulę:
von Neumann architektūra= atstumas[i][j] = mažiausias (atstumas[i][j], (atstumas nuo i iki IR ) + (Atstumas nuo IR į j))
= atstumas[i][j] = mažiausias (atstumas[i][j], atstumas[i][ IR ] + atstumas[ IR ][j])7 veiksmas : Kadangi visi mazgai buvo traktuojami kaip tarpiniai mazgai, dabar kaip atsakymo matricą galime grąžinti atnaujintą atstumo[][] matricą.
Toliau pateikiamas pirmiau minėto metodo įgyvendinimas:
C++ // C++ Program for Floyd Warshall Algorithm #include using namespace std; // Number of vertices in the graph #define V 4 /* Define Infinite as a large enough value.This value will be used for vertices not connected to each other */ #define INF 99999 // A function to print the solution matrix void printSolution(int dist[][V]); // Solves the all-pairs shortest path // problem using Floyd Warshall algorithm void floydWarshall(int dist[][V]) { int i, j, k; /* Add all vertices one by one to the set of intermediate vertices. --->Prieš pradedant iteraciją, mes turime trumpiausius atstumus tarp visų viršūnių porų, kad trumpiausi atstumai laiko tarpinėmis viršūnėmis tik aibės {0, 1, 2, .. k-1} viršūnes. ----> Pasibaigus iteracijai, viršūnė Nr. k pridedama prie tarpinių viršūnių aibės ir aibė tampa {0, 1, 2, .. k} */, kai (k = 0; k< V; k++) { // Pick all vertices as source one by one for (i = 0; i < V; i++) { // Pick all vertices as destination for the // above picked source for (j = 0; j < V; j++) { // If vertex k is on the shortest path from // i to j, then update the value of // dist[i][j] if (dist[i][j]>(dist[i][k] + dist[k][j]) && (dist[k][j] != INF && dist[i][k] != INF)) dist[i][j] = dist[i][k] + dist[k][j]; } } } // Spausdinti trumpiausio atstumo matricą printSolution(dist); } /* Naudingumo funkcija sprendimui spausdinti */ void printSolution(int dist[][V]) { cout<< 'The following matrix shows the shortest ' 'distances' ' between every pair of vertices
'; for (int i = 0; i < V; i++) { for (int j = 0; j < V; j++) { if (dist[i][j] == INF) cout << 'INF' << ' '; else cout << dist[i][j] << ' '; } cout << endl; } } // Driver's code int main() { /* Let us create the following weighted graph 10 (0)------->(3) | /| 5 | | | | 1 |/ | (1)------->(2) 3 */ int grafikas[V][V] = { { 0, 5, INF, 10 }, { INF, 0, 3, INF }, { INF, INF, 0, 1 }, { INF, INF, INF, 0} }; // Funkcijos iškvietimas floydWarshall(graph); grąžinti 0; } // Šį kodą sukūrė Mythri J L>>C(3) | /| 5 | | | | 1 |/ | (1)------->(2) 3 */ int grafikas[V][V] = { { 0, 5, INF, 10 }, { INF, 0, 3, INF }, { INF, INF, 0, 1 }, { INF, INF, INF, 0} }; // Funkcijos iškvietimas floydWarshall(graph); grąžinti 0; }> Java // Java program for Floyd Warshall All Pairs Shortest // Path algorithm. import java.io.*; import java.lang.*; import java.util.*; class AllPairShortestPath { final static int INF = 99999, V = 4; void floydWarshall(int dist[][]) { int i, j, k; /* Add all vertices one by one to the set of intermediate vertices. --->Prieš pradedant iteraciją, mes turime trumpiausius atstumus tarp visų viršūnių porų, kad trumpiausi atstumai laiko tarpinėmis viršūnėmis tik aibės {0, 1, 2, .. k-1} viršūnes. ----> Pasibaigus iteracijai, viršūnė Nr. k pridedama prie tarpinių viršūnių aibės ir aibė tampa {0, 1, 2, .. k} */, kai (k = 0; k< V; k++) { // Pick all vertices as source one by one for (i = 0; i < V; i++) { // Pick all vertices as destination for the // above picked source for (j = 0; j < V; j++) { // If vertex k is on the shortest path // from i to j, then update the value of // dist[i][j] if (dist[i][k] + dist[k][j] < dist[i][j]) dist[i][j] = dist[i][k] + dist[k][j]; } } } // Print the shortest distance matrix printSolution(dist); } void printSolution(int dist[][]) { System.out.println( 'The following matrix shows the shortest ' + 'distances between every pair of vertices'); for (int i = 0; i < V; ++i) { for (int j = 0; j < V; ++j) { if (dist[i][j] == INF) System.out.print('INF '); else System.out.print(dist[i][j] + ' '); } System.out.println(); } } // Driver's code public static void main(String[] args) { /* Let us create the following weighted graph 10 (0)------->(3) | /| 5 | | | | 1 |/ | (1)------->(2) 3 */ int graph[][] = { { 0, 5, INF, 10 }, { INF, 0, 3, INF }, { INF, INF, 0, 1 }, { INF, INF, INF, 0 } }; AllPairShortestPath a = new AllPairShortestPath(); // Funkcijos iškvietimas a.floydWarshall(graph); } } // Prisidėjo Aakash Hasija>>Python3Prieš pradedant iteraciją, mes turime trumpiausius atstumus tarp visų viršūnių porų, kad tarpinėmis viršūnėmis būtų laikomos tik aibės {0, 1, 2, .. k-1} viršūnės. ----> Pasibaigus iteracijai, viršūnė Nr. k pridedamas prie tarpinių viršūnių aibės ir aibė tampa {0, 1, 2, .. k} ''' k diapazone (V): # pasirinkite visas viršūnes kaip šaltinį po vieną, kai i in diapazonas (V): # Pasirinkite visas viršūnes kaip paskirties vietą # aukščiau pasirinktam j šaltiniui diapazone (V): # Jei viršūnė k yra trumpiausiame kelyje nuo # i iki j, tada atnaujinkite dist[i][ j] dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j] ) printSolution(dist) # Naudingumo funkcija, skirta spausdinti sprendimą def printSolution (dist): print ('Sekančioje matricoje rodomi trumpiausi atstumai tarp kiekvienos viršūnių poros') i diapazone (V): j diapazone (V): if(dist[i][j] == INF): print('%7s' % ('INF'), end=' ') else: print('%7d ' % (dist[i][j]), end=' ') if j == V-1: print() # Tvarkyklės kodas if __name__ == '__main__': ''' 10 (0)------ ->(3) | /| 5 | | | | 1 |/ | (1)------->(2) 3 ''' grafikas = [[0, 5, INF, 10], [INF, 0, 3, INF], [INF, INF, 0 , 1], [INF, INF, INF, 0] ] # Funkcijų iškvietimas floydWarshall(graph) # Šį kodą sukūrė Mythri J L> C# // C# program for Floyd Warshall All // Pairs Shortest Path algorithm. using System; public class AllPairShortestPath { readonly static int INF = 99999, V = 4; void floydWarshall(int[, ] graph) { int[, ] dist = new int[V, V]; int i, j, k; // Initialize the solution matrix // same as input graph matrix // Or we can say the initial // values of shortest distances // are based on shortest paths // considering no intermediate // vertex for (i = 0; i < V; i++) { for (j = 0; j < V; j++) { dist[i, j] = graph[i, j]; } } /* Add all vertices one by one to the set of intermediate vertices. --->Prieš pradedant iteraciją, mes turime trumpiausius atstumus tarp visų viršūnių porų, kad trumpiausi atstumai laiko tarpinėmis viršūnėmis tik aibės {0, 1, 2, .. k-1} viršūnes. ---> Pasibaigus iteracijai, viršūnė Nr. k pridedama prie tarpinių viršūnių aibės ir aibė tampa {0, 1, 2, .. k} */, kai (k = 0; k< V; k++) { // Pick all vertices as source // one by one for (i = 0; i < V; i++) { // Pick all vertices as destination // for the above picked source for (j = 0; j < V; j++) { // If vertex k is on the shortest // path from i to j, then update // the value of dist[i][j] if (dist[i, k] + dist[k, j] < dist[i, j]) { dist[i, j] = dist[i, k] + dist[k, j]; } } } } // Print the shortest distance matrix printSolution(dist); } void printSolution(int[, ] dist) { Console.WriteLine( 'Following matrix shows the shortest ' + 'distances between every pair of vertices'); for (int i = 0; i < V; ++i) { for (int j = 0; j < V; ++j) { if (dist[i, j] == INF) { Console.Write('INF '); } else { Console.Write(dist[i, j] + ' '); } } Console.WriteLine(); } } // Driver's Code public static void Main(string[] args) { /* Let us create the following weighted graph 10 (0)------->(3) | /| 5 | | | | 1 |/ | (1)------->(2) 3 */ int[, ] grafikas = { { 0, 5, INF, 10 }, { INF, 0, 3, INF }, { INF, INF, 0 , 1 }, { INF, INF, INF, 0 } }; AllPairShortestPath a = new AllPairShortestPath(); // Funkcijos iškvietimas a.floydWarshall(graph); } } // Šio straipsnio autorius // Abdul Mateen Mohammed>>Javascript(3) | /| 5 | | | | 1 |/ | (1)------->(2) 3 */ var graph = [ [0, 5, INF, 10], [INF, 0, 3, INF], [INF, INF, 0, 1] , [INF, INF, INF, 0], ]; var a = new AllPairShortestPath(); // Spausdinti sprendimą a.floydWarshall(graph); // Šį kodą sukūrė rdtaank.>> PHP(3) | /| 5 | | | | 1 |/ | (1)------->(2) 3 */ $graph = masyvas(masyvas(0, 5, $INF, 10), masyvas($INF, 0, 3, $INF), masyvas($ INF, $INF, 0, 1), masyvas ($INF, $INF, $INF, 0)); // Funkcijos iškvietimas floydWarshall($graph, $V, $INF); // Šį kodą sukūrė Ryuga ?>>>
Išvestis Floydo Warshall algoritmo sudėtingumo analizė: - Laiko sudėtingumas: O(V3), kur V yra grafiko viršūnių skaičius ir vykdome tris įdėtas V dydžio kilpas
- Pagalbinė erdvė: O(V2), sukurti 2-D matricą, kad būtų išsaugotas trumpiausias kiekvienos mazgų poros atstumas.
Pastaba : Aukščiau pateikta programa spausdina tik trumpiausius atstumus. Mes galime modifikuoti sprendimą, kad būtų spausdinami trumpiausi keliai, taip pat išsaugodami pirmtako informaciją atskiroje 2D matricoje.
Kodėl Floydo-Warshall algoritmas tinka tankiems, o ne retiems grafikams?
Tankus grafikas : grafikas, kuriame briaunų skaičius yra žymiai didesnis už viršūnių skaičių.
Retas grafikas : grafikas, kuriame kraštinių skaičius yra labai mažas.
Nesvarbu, kiek kraštinių yra grafike Floydo Warshall algoritmas eina už O(V3) kartus, todėl jis geriausiai tinka Tankūs grafikai . Retų grafikų atveju Johnsono algoritmas yra tinkamesnis.
Svarbūs interviu klausimai, susiję su Floyd-Warshall:
- Kaip aptikti neigiamą ciklą grafike naudojant Floydo Warshall algoritmą?
- Kuo Floydo-warshall algoritmas skiriasi nuo Dijkstros algoritmo?
- Kuo Floyd-Warshall algoritmas skiriasi nuo Bellman-Ford algoritmo?
Floydo-Warshall algoritmo taikymas realiame pasaulyje:
- Kompiuterių tinkle algoritmas gali būti naudojamas norint rasti trumpiausią kelią tarp visų tinklo mazgų porų. Tai vadinama kaip tinklo maršruto parinkimas .
- Skrydžių sujungimas Aviacijos pramonėje ieškoma trumpiausio kelio tarp oro uostų.
- GIS ( Geografinės informacinės sistemos ) programos dažnai apima erdvinių duomenų, pvz., kelių tinklų, analizę, kad būtų galima rasti trumpiausius kelius tarp vietų.
- Kleene'o algoritmas kuris yra floyd warshall apibendrinimas, gali būti naudojamas ieškant įprastos kalbos reguliariosios išraiškos.