Atsižvelgiant į a specialus dvejetainis medis kurių lapų mazgai yra sujungti į formą a apskritas dvigubai susietas sąrašas užduotis yra surasti aukščio medžio.
Pavyzdžiai:
Įvestis:

Išvestis: 2
Paaiškinimas: Dvejetainio medžio aukštis atpažinus lapų mazgus yra 2. Aukščiau pateiktame dvejetainiame medyje 6 5 ir 4 yra lapų mazgai ir jie sudaro apskritą dvigubai susietą sąrašą. Čia kairioji lapo mazgo rodyklė veiks kaip ankstesnė apskrito dvigubai susieto sąrašo rodyklė, o dešinė – kaip kita apskrito dvigubai susieto sąrašo rodyklė.Įvestis:
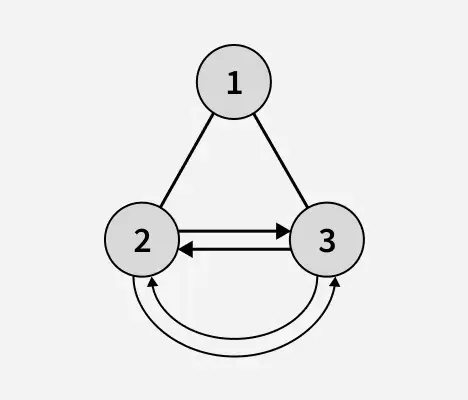
Išvestis: 1
Paaiškinimas: Dvejetainio medžio aukštis atpažinus lapų mazgus yra 1. Aukščiau pateiktame dvejetainiame medyje 2 ir 3 yra lapų mazgai ir jie sudaro apskritą, dvigubai susietą sąrašą.kas yra 10 iš 100
Prieiga :
C++Idėja yra sekti panašus požiūris kaip mes darome įprasto dvejetainio medžio aukščio radimas . Mes rekursyviai apskaičiuoti aukščio iš kairėn ir dešinėn mazgo pomedžiai ir priskirti aukščio prie mazgo as maks dviejų vaikų ūgio plius 1. Bet kairysis ir dešinysis vaikas a lapo mazgas normaliems dvejetainiams medžiams yra nuliniai. Bet čia lapo mazgas yra apskritas, dvigubai susietas sąrašo mazgas. Taigi, kad mazgas būtų lapo mazgas, patikriname, ar mazgas kairėje dešinėje rodo į mazgas ir jos dešinė kairė taip pat nurodo į mazgas pati.
// C++ program to calculate height of a special tree // whose leaf nodes forms a circular doubly linked list #include
// C program to calculate height of a special tree // whose leaf nodes forms a circular doubly linked list #include
// Java program to calculate height of a special tree // whose leaf nodes forms a circular doubly linked list class Node { int data; Node left right; Node(int x) { data = x; left = null; right = null; } } class GfG { // function to check if given // node is a leaf node or node static boolean isLeaf(Node node) { // For a node to be a leaf node it should // satisfy the following two conditions: // 1. Node's left's right pointer should be // current node. // 2. Node's right's left pointer should be // current node. // If one condition is met it is guaranteed // that the other condition is also true. return node.left != null && node.left.right == node && node.right != null && node.right.left == node; } // Compute the height of a tree static int findTreeHeight(Node node) { // if node is NULL return -1. if (node == null) return -1; // if node is a leaf node return 0 if (isLeaf(node)) return 0; // compute the depth of each subtree and take maximum return 1 + Math.max(findTreeHeight(node.left) findTreeHeight(node.right)); } public static void main(String[] args) { Node root = new Node(1); root.left = new Node(2); root.right = new Node(3); root.left.left = new Node(4); root.left.right = new Node(5); root.left.left.left = new Node(6); // Given tree contains 3 leaf nodes Node l1 = root.left.left.left; Node l2 = root.left.right; Node l3 = root.right; // create circular doubly linked list out of // leaf nodes of the tree // set next pointer of linked list l1.right = l2; l2.right = l3; l3.right = l1; // set prev pointer of linked list l3.left = l2; l2.left = l1; l1.left = l3; System.out.println(findTreeHeight(root)); } }
# Python program to calculate height of a special tree # whose leaf nodes forms a circular doubly linked list class Node: def __init__(self data): self.data = data self.left = None self.right = None # function to check if given # node is a leaf node or node def isLeaf(node): # For a node to be a leaf node it should # satisfy the following two conditions: # 1. Node's left's right pointer should be # current node. # 2. Node's right's left pointer should be # current node. # If one condition is met it is guaranteed # that the other condition is also true. return (node.left and node.left.right == node and node.right and node.right.left == node) # Compute the height of a tree def findTreeHeight(node): # if node is NULL return -1. if node is None: return -1 # if node is a leaf node return 0 if isLeaf(node): return 0 # compute the depth of each subtree and take maximum return 1 + max(findTreeHeight(node.left) findTreeHeight(node.right)) if __name__ == '__main__': root = Node(1) root.left = Node(2) root.right = Node(3) root.left.left = Node(4) root.left.right = Node(5) root.left.left.left = Node(6) # Given tree contains 3 leaf nodes l1 = root.left.left.left l2 = root.left.right l3 = root.right # create circular doubly linked list out of # leaf nodes of the tree # set next pointer of linked list l1.right = l2 l2.right = l3 l3.right = l1 # set prev pointer of linked list l3.left = l2 l2.left = l1 l1.left = l3 print(findTreeHeight(root))
// C# program to calculate height of a special tree // whose leaf nodes forms a circular doubly linked list using System; class Node { public int data; public Node left right; public Node(int x) { data = x; left = null; right = null; } } class GfG { // function to check if given // node is a leaf node or node static bool isLeaf(Node node) { // For a node to be a leaf node it should // satisfy the following two conditions: // 1. Node's left's right pointer should be // current node. // 2. Node's right's left pointer should be // current node. // If one condition is met it is guaranteed // that the other condition is also true. return node.left != null && node.left.right == node && node.right != null && node.right.left == node; } // Compute the height of a tree static int findTreeHeight(Node node) { // if node is NULL return -1. if (node == null) return -1; // if node is a leaf node return 0 if (isLeaf(node)) return 0; // compute the depth of each subtree and take maximum return 1 + Math.Max(findTreeHeight(node.left) findTreeHeight(node.right)); } static void Main(string[] args) { Node root = new Node(1); root.left = new Node(2); root.right = new Node(3); root.left.left = new Node(4); root.left.right = new Node(5); root.left.left.left = new Node(6); // Given tree contains 3 leaf nodes Node l1 = root.left.left.left; Node l2 = root.left.right; Node l3 = root.right; // create circular doubly linked list out of // leaf nodes of the tree // set next pointer of linked list l1.right = l2; l2.right = l3; l3.right = l1; // set prev pointer of linked list l3.left = l2; l2.left = l1; l1.left = l3; Console.WriteLine(findTreeHeight(root)); } }
// JavaScript program to calculate height of a special tree // whose leaf nodes forms a circular doubly linked list class Node { constructor(data) { this.data = data; this.left = null; this.right = null; } } // function to check if given // node is a leaf node or node function isLeaf(node) { // For a node to be a leaf node it should // satisfy the following two conditions: // 1. Node's left's right pointer should be // current node. // 2. Node's right's left pointer should be // current node. // If one condition is met it is guaranteed // that the other condition is also true. return node.left && node.left.right === node && node.right && node.right.left === node; } // Compute the height of a tree function findTreeHeight(node) { // if node is NULL return -1. if (node === null) return -1; // if node is a leaf node return 0 if (isLeaf(node)) return 0; // compute the depth of each subtree and take maximum return 1 + Math.max(findTreeHeight(node.left) findTreeHeight(node.right)); } const root = new Node(1); root.left = new Node(2); root.right = new Node(3); root.left.left = new Node(4); root.left.right = new Node(5); root.left.left.left = new Node(6); // Given tree contains 3 leaf nodes const l1 = root.left.left.left; const l2 = root.left.right; const l3 = root.right; // create circular doubly linked list out of // leaf nodes of the tree // set next pointer of linked list l1.right = l2; l2.right = l3; l3.right = l1; // set prev pointer of linked list l3.left = l2; l2.left = l1; l1.left = l3; console.log(findTreeHeight(root));
Išvestis
3
Laiko sudėtingumas: O(n) kur n yra mazgų skaičius.
Pagalbinė erdvė: O(h)


