Posakių medis yra medis, naudojamas įvairioms išraiškoms pavaizduoti. Medžio duomenų struktūra naudojama išraiškiniams teiginiams pavaizduoti. Šiame medyje vidinis mazgas visada žymi operatorius.
- Lapų mazgai visada žymi operandus.
- Veiksmai visada atliekami su šiais operandais.
- Medžio gilumoje esantis operatorius visada turi aukščiausią prioritetą.
- Operatorius, kurio gylyje medyje nėra daug, visada turi mažiausią prioritetą, palyginti su operatoriais, gulinčiais gylyje.
- Operandas visada bus pateiktas medžio gylyje; todėl jis laikomas aukščiausias prioritetas tarp visų operatorių.
- Trumpai tariant, galime tai apibendrinti, nes medžio gylyje esanti vertė turi didžiausią prioritetą, palyginti su kitais medžio viršuje esančiais operatoriais.
- Pagrindinis šių išraiškos medžių panaudojimas yra tai, kad jis yra įpratęs vertinti, analizuoti ir modifikuoti įvairios išraiškos.
- Jis taip pat naudojamas norint išsiaiškinti kiekvieno operatoriaus asociatyvumą išraiškoje.
- Pavyzdžiui, + operatorius yra kairysis asociatyvus ir / yra dešinysis asociatyvus.
- Šio asociatyvumo dilema buvo išspręsta naudojant išraiškų medžius.
- Šie išraiškų medžiai sudaromi naudojant bekontekstinę gramatiką.
- Mes susiejome taisyklę bekontekstinėse gramatikose prieš kiekvieną gramatikos gaminį.
- Šios taisyklės taip pat žinomos kaip semantinės taisyklės, o naudodami šias semantines taisykles galime lengvai sukurti išraiškų medžius.
- Tai viena iš pagrindinių kompiliatoriaus dizaino dalių ir priklauso semantinės analizės fazei.
- Šioje semantinėje analizėje naudosime į sintaksę nukreiptus vertimus, o išvesties pavidalu sukursime anotuotą analizavimo medį.
- Anotuotas analizės medis yra ne kas kita, kaip paprasta analizė, susijusi su tipo atributu ir kiekviena gamybos taisykle.
- Pagrindinis išraiškų medžių naudojimo tikslas yra sukurti sudėtingas išraiškas, kurias galima lengvai įvertinti naudojant šiuos išraiškų medžius.
- Jis yra nekintamas, ir sukūrę išraiškų medį, negalime jo keisti ar toliau modifikuoti.
- Norint atlikti daugiau modifikacijų, reikia visiškai sukurti naują išraiškų medį.
- Jis taip pat naudojamas sprendžiant postfikso, priešdėlio ir infikso išraiškos vertinimą.
Išraiškos medžiai vaidina labai svarbų vaidmenį reprezentuojant kalbos lygiu kodą duomenų pavidalu, kurie daugiausia saugomi į medį panašioje struktūroje. Jis taip pat naudojamas vaizduojant atmintį lambda išraiška. Naudojant medžio duomenų struktūrą, lambda išraišką galime išreikšti skaidriau ir aiškiau. Pirmiausia jis sukuriamas konvertuoti kodo segmentą į duomenų segmentą, kad išraišką būtų galima lengvai įvertinti.
Išraiškos medis yra dvejetainis medis, kuriame kiekvienas išorinis arba lapo mazgas atitinka operandą, o kiekvienas vidinis arba pirminis mazgas atitinka operatorius, taigi, pavyzdžiui, išraiškos medis 7 + ((1+8)*3) būtų toks:
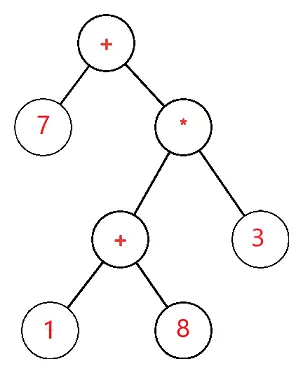
Tegul S yra išraiškos medis
Jei S nėra nulis, tada
Jei S.value yra operandas, tada
Grąžinti S.vertę
x = išspręsti (S.kairėje)
y = išspręsti (S.dešinė)
Grąžos skaičiavimas(x, y, S.reikšmė)
Aukščiau pateiktame pavyzdyje išraiškų medis naudojo bekontekstinę gramatiką.
Šioje gramatikoje yra keletas kūrinių, susijusių su kai kuriomis gamybos taisyklėmis, daugiausia žinomų kaip semantines taisykles . Naudodami šias semantines taisykles galime apibrėžti rezultato kūrimą pagal atitinkamas gamybos taisykles. Čia mes panaudojome reikšmės parametrą, kuris apskaičiuos rezultatą ir grąžins jį į gramatikos pradžios simbolį. S.left apskaičiuos kairįjį mazgo atžalą ir panašiai, naudojant S.right parametrą, galima apskaičiuoti ir dešinįjį mazgo antrį.
Išraiškų medžio naudojimas
- Pagrindinis išraiškų medžių naudojimo tikslas yra sukurti sudėtingas išraiškas, kurias galima lengvai įvertinti naudojant šiuos išraiškų medžius.
- Jis taip pat naudojamas norint išsiaiškinti kiekvieno operatoriaus asociatyvumą išraiškoje.
- Jis taip pat naudojamas sprendžiant postfikso, priešdėlio ir infikso išraiškos vertinimą.
Išraiškų medžio įgyvendinimas
Norėdami įgyvendinti išraiškų medį ir parašyti jo programą, turėsime naudoti kamino duomenų struktūrą.
Kadangi žinome, kad dėklas yra pagrįstas LIFO principu, paskutinis iš pradžių, duomenų elementas, neseniai įstumtas į krūvą, buvo iššokamas, kai tik reikia. Jo įgyvendinimui naudojamos dvi pagrindinės kamino operacijos - stumti ir pop. Naudodami stūmimo operaciją duomenų elementą įstumsime į krūvą, o naudodami pop operaciją išimsime duomenų elementą iš krūvos.
Pagrindinės krūvos funkcijos išraiškų medžio įgyvendinime:
Pirmiausia nuskaitysime pateiktą išraišką iš kairės į dešinę, tada po vieną patikrinsime identifikuotą simbolį,
- Jei nuskaitytas simbolis yra operandas, taikysime stūmimo operaciją ir įstumsime jį į krūvą.
- Jei nuskaitytas simbolis yra operatorius, jame taikysime iššokimo operaciją, kad pašalintume dvi reikšmes iš krūvos, kad jos taptų antrinėmis, o po to dabartinį pirminį mazgą sugrąžinsime į krūvą.
Išraiškų medžio įgyvendinimas C programavimo kalba
// C program for expression tree implementation #include #include /* The below structure node is defined as a node of a binary tree consists of left child and the right child, along with the pointer next which points to the next node */ struct node { char info ; struct node* l ; struct node* r ; struct node* nxt ; }; struct node *head=NULL; /* Helper function that allocates a new node with the given data and NULL left and right pointers. */ struct node* newnode(char data) { struct node* node = (struct node*) malloc ( sizeof ( struct node ) ) ; node->info = data ; node->l = NULL ; node->r = NULL ; node->nxt = NULL ; return ( node ) ; } void Inorder(struct node* node) { if ( node == NULL) return ; else { /* first recur on left child */ Inorder ( node->l ) ; /* then print the data of node */ printf ( '%c ' , node->info ) ; /* now recur on right child */ Inorder ( node->r ) ; } } void push ( struct node* x ) { if ( head == NULL ) head = x ; else { ( x )->nxt = head ; head = x ; } // struct node* temp ; // while ( temp != NULL ) // { // printf ( ' %c ' , temp->info ) ; // temp = temp->nxt ; // } } struct node* pop() { // Poping out the top most [pointed with head] element struct node* n = head ; head = head->nxt ; return n ; } int main() { char t[] = { 'X' , 'Y' , 'Z' , '*' , '+' , 'W' , '/' } ; int n = sizeof(t) / sizeof(t[0]) ; int i ; struct node *p , *q , *s ; for ( i = 0 ; i <n ; i++ ) { if read character is operator then popping two other elements from stack and making a binary tree ( t[i]="=" '+' || '-' '*' ' '^' s="newnode" t [ i ] p="pop()" q="pop()" s->l = q ; s->r = p; push(s); } else { s = newnode ( t [ i ] ) ; push ( s ) ; } } printf ( ' The Inorder Traversal of Expression Tree: ' ) ; Inorder ( s ) ; return 0 ; } </n> Aukščiau pateiktos programos rezultatas yra:
X + Y * Z / W
Išraiškų medžio įgyvendinimas C++ programavimo kalba
// C++ program for expression tree #include using namespace std ; /* The below class node is defined as a node of a binary tree consists of left child and the right child, along with the pointer next which points to the next node */ class node { public: char info ; node* l ; node* r ; node* nxt = NULL ; node ( char c ) { this->info = c ; l = NULL ; r = NULL ; } node() { l = NULL ; r = NULL ; } friend class Stack ; friend class tree ; } ; class Stack { node* head = NULL ; public: void push ( node* ) ; node* pop() ; friend class tree ; } ; class tree { public: void inorder ( node* x ) { // cout<<'tree in inorder traversal is: '<l ) ; cout <info <r } void stack::push( node* x { if ( head="=" null we are inserting here nodes at the top of stack [following lifo principle] else x->nxt = head ; head = x ; } } node* Stack::pop() { // Poping out the top most [ pointed with head ] element node* p = head ; head = head->nxt ; return p ; } int main() { string str = 'XYZ*+W/' ; // If you wish take input from user: //cout << 'Insert Postorder Expression: ' <> s; Stack s ; tree t ; node *p, *q, *re; int n = str.length() ; for ( int i = 0 ; i <n ; i++ ) { if ( str[ i ]="=" '+' || '-' '*' ' '^') re="new" node( str[i] p="s.pop()" q="s.pop()" re->l = q ; re->r = p ; s.push(re) ; } else { re = new node( str[ i ] ) ; s.push(re) ; } } cout << ' The Inorder Traversal of Expression Tree: ' ; t.inorder(re) ; return 0 ; } </n></'tree> Aukščiau pateiktos programos išvestis yra tokia:
X + Y * Z / W
Išraiškų medžio diegimas Java programavimo kalba
// Java program for expression tree import java.util.* ; /* The below class node is defined as a node of a binary tree consists of left child and the right child, along with the pointer next which points to the next node */ class Node { char info ; Node l , r ; public Node(char data) { this.info = data ; l = null ; r = null ; } } public class Main { public static boolean isOperator ( char ch ) { if ( ch == '+' || ch == '-' || ch == '*' || ch == '/' || ch == '^' ) { return true ; } return false ; } public static Node Tree ( String postfix ) { Stack st = new Stack(); Node t1,t2,temp ; for ( int i = 0 ; i <p> <strong>The output of the above program is:</strong> </p> <pre> X + Y * Z / W </pre> <hr> 