Įterpimo rūšiavimas ir pasirinkimo rūšiavimas yra du populiarūs rūšiavimo algoritmai, o pagrindinis jų skirtumas slypi tame, kaip jie pasirenka ir išdėsto elementus rūšiuotoje sekoje.
Pasirinkimo rūšiavimas:
- Atrankos rūšiavimo metu įvesties masyvas yra padalintas į dvi dalis: surūšiuotą ir nerūšiuotą dalį.
- Algoritmas pakartotinai suranda minimalų elementą nerūšiuotoje dalyje ir sukeičia jį į kairiausią nerūšiuotos dalies elementą, taip išplėsdamas surūšiuotą dalį vienu elementu.
- Pasirinkimo rūšiavimo laiko sudėtingumas visais atvejais yra O(n^2).
Įterpimo rūšiavimas:
- Įterpimo rūšiavimo metu įvesties masyvas taip pat yra padalintas į dvi dalis: surūšiuotą ir nerūšiuotą dalį.
Algoritmas paima elementą iš nerūšiuotos dalies ir įdeda jį į teisingą rūšiuojamos dalies vietą, didesnius elementus perkeldamas viena pozicija į dešinę.
Įterpimo rūšiavimo laiko sudėtingumas blogiausiu atveju yra O(n^2), bet gali geriau veikti iš dalies surūšiuotuose masyvuose, o geriausiu atveju laiko sudėtingumas yra O(n).
Pagrindiniai skirtumai: - Pasirinkimo rūšiavimas nuskaito nerūšiuotą dalį, kad surastų mažiausią elementą, o įterpimo rūšiavimas nuskaito surūšiuotą dalį, kad surastų tinkamą vietą elementui įdėti.
Pasirinkimo rūšiavimui reikia mažiau apsikeitimų nei įterpimo rūšiavimo, bet daugiau palyginimų.
Įterpimo rūšiavimas yra efektyvesnis nei pasirinkimo rūšiavimas, kai įvesties masyvas yra iš dalies arba beveik surūšiuotas, o pasirinkimo rūšiavimas veikia geriau, kai masyvas yra labai nerūšiuotas.
Apibendrinant galima pasakyti, kad abu algoritmai turi panašų laiko sudėtingumą, tačiau skiriasi jų pasirinkimo ir išdėstymo metodai. Pasirinkimas tarp jų priklauso nuo įvesties duomenų ypatybių ir konkrečių nagrinėjamos problemos reikalavimų.
Įterpimo rūšiavimo pranašumai:
- Paprasta ir lengvai suprantama bei įgyvendinama.
- Veiksmingas mažiems duomenų rinkiniams arba beveik surūšiuotiems duomenims.
- Rūšiavimo vietoje algoritmas, tai reiškia, kad jam nereikia papildomos atminties.
- Stabilus rūšiavimo algoritmas, reiškiantis, kad jis palaiko santykinę vienodų elementų tvarką įvesties masyve.
Įterpimo rūšiavimo trūkumai:
- Neefektyvus dideliems duomenų rinkiniams arba atvirkštinės eilės duomenims, o blogiausiu atveju laiko sudėtingumas yra O(n^2).
- Įterpimo rūšiavimas turi daug apsikeitimų, todėl šiuolaikiniuose kompiuteriuose jis gali sulėtinti.
Pasirinkimo rūšiavimo pranašumai:
- Paprasta ir lengvai suprantama bei įgyvendinama.
- Veiksmingas mažiems duomenų rinkiniams arba beveik surūšiuotiems duomenims.
- Rūšiavimo vietoje algoritmas, tai reiškia, kad jam nereikia papildomos atminties.
Pasirinkimo rūšiavimo trūkumai:
- Neefektyvus dideliems duomenų rinkiniams, o blogiausiu atveju laiko sudėtingumas yra O(n^2).
- Pasirinkimo rūšiavimas turi daug palyginimų, todėl šiuolaikiniuose kompiuteriuose jis gali sulėtėti.
- Nestabilus rūšiavimo algoritmas, ty jis gali nepalaikyti santykinės vienodų elementų tvarkos įvesties masyve.
Šiame straipsnyje aptarsime skirtumą tarp įterpimo rūšiavimo ir pasirinkimo rūšiavimo:
Įterpimo rūšiavimas yra paprastas rūšiavimo algoritmas, kuris veikia panašiai kaip rūšiuojate žaidimo kortas jūsų rankose. Masyvas yra beveik padalintas į surūšiuotą ir nerūšiuotą dalis. Vertės iš nerūšiuotos dalies parenkamos ir pateikiamos tinkamoje surūšiuotos dalies vietoje.
Algoritmas:
Norėdami rūšiuoti n dydžio masyvą didėjančia tvarka:
- Per masyvą kartokite nuo arr[1] iki arr[n].
- Palyginkite dabartinį elementą (raktą) su jo pirmtaku.
- Jei pagrindinis elementas yra mažesnis nei jo pirmtakas, palyginkite jį su ankstesniais elementais. Perkelkite didesnius elementus viena pozicija aukštyn, kad būtų vietos pakeistam elementui.
Žemiau pateikiamas paveikslėlis, iliustruojantis įterpimo rūšiavimą:
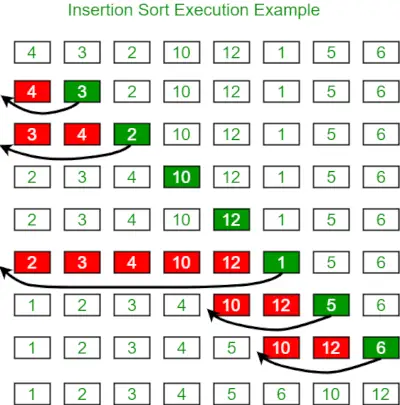
Žemiau yra tos pačios programos:
C++
// C++ program for the insertion sort> #include> using> namespace> std;> // Function to sort an array using> // insertion sort> void> insertionSort(>int> arr[],>int> n)> {> >int> i, key, j;> >for> (i = 1; i key = arr[i]; j = i - 1; // Move elements of arr[0..i-1], // that are greater than key to // one position ahead of their // current position while (j>= 0 && arr[j]> klavišas) { arr[j + 1] = arr[j]; j = j - 1; } arr[j + 1] = raktas; } } // Funkcija spausdinti N dydžio masyvą void printArray(int arr[], int n) { int i; // Spausdinti masyvą (i = 0; i cout<< arr[i] << ' '; } cout << endl; } // Driver Code int main() { int arr[] = { 12, 11, 13, 5, 6 }; int N = sizeof(arr) / sizeof(arr[0]); // Function Call insertionSort(arr, N); printArray(arr, N); return 0; }> |
>
>
Java
// Java program for the above approach> import> java.util.*;> class> GFG> {> > // Function to sort an array using> // insertion sort> static> void> insertionSort(>int> arr[],>int> n)> {> >int> i, key, j;> >for> (i =>1>; i { key = arr[i]; j = i - 1; // Move elements of arr[0..i-1], // that are greater than key to // one position ahead of their // current position while (j>= 0 && arr[j]> raktas) { arr[j + 1] = arr[j]; j = j - 1; } arr[j + 1] = raktas; } } // Funkcija spausdinti N dydžio masyvą static void printArray(int arr[], int n) { int i; // Spausdinti masyvą (i = 0; i System.out.print(arr[i] + ' '); } System.out.println(); } // Tvarkyklės kodas public static void main(String[ ] args) { int arr[] = { 12, 11, 13, 5, 6 }; Šį kodą sukūrė code_hunt>> |
>
# Python 3 program for the insertion sort># Function to sort an array using># insertion sort>def>insertionSort(arr, n):>>i>=>0>>key>=>0>>j>=>0>>for>i>in>range>(>1>,n,>1>):>>key>=>arr[i]>>j>=>i>->1>># Move elements of arr[0..i-1],>># that are greater than key to>># one position ahead of their>># current position>>while>(j>>>0> and>arr[j]>raktas):>>arr[j>+>1>]>=>arr[j]>>j>=>j>->1>>arr[j>+>1>]>=>key># Function to print an array of size N>def>printArray(arr, n):>>i>=>0>># Print the array>>for>i>in>range>(n):>>print>(arr[i],end>=>' '>)>>print>(>' '>,end>=>'')># Driver Code>if>__name__>=>=>'__main__'>:>>arr>=>[>12>,>11>,>13>,>5>,>6>]>>N>=>len>(arr)>># Function Call>>insertionSort(arr, N)>>printArray(arr, N)>>># This code is contributed by bgangwar59.>>>C#
// C# program for the above approach>using>System;>class>GFG>{>>// Function to sort an array using>>// insertion sort>>static>void>insertionSort(>int>[] arr,>int>n)>>{>>int>i, key, j;>>for>(i = 1; i { key = arr[i]; j = i - 1; // Move elements of arr[0..i-1], // that are greater than key to // one position ahead of their // current position while (j>= 0 && arr[j]> raktas) { arr[j + 1] = arr[j]; j = j - 1; } arr[j + 1] = raktas; } } // Funkcija spausdinti N dydžio masyvą static void printArray(int[] arr, int n) { int i; // Spausdinti masyvą (i = 0; i { Console.Write(arr[i] + ' '); } Console.WriteLine(); } // Tvarkyklės kodas statinis public void Main() { int[] arr = new int[] { 12, 11, 13, 5, 6 } int N = arr.Length; prisidėjo Dharanendra L V>>>Javascript
>// JavaScript program for the above approach>// Function to sort an array using>// insertion sort>function>insertionSort(arr,n)>{>>let i, key, j;>>for>(i = 1; i { key = arr[i]; j = i - 1; // Move elements of arr[0..i-1], // that are greater than key to // one position ahead of their // current position while (j>= 0 && arr[j]> raktas) { arr[j + 1] = arr[j]; j = j - 1; } arr[j + 1] = raktas; } } // Funkcija spausdinti N dydžio masyvą function printArray(arr,n) { let i; // Spausdinti masyvą (i = 0; i document.write(arr[i] + ' '); } document.write(' '); } // Tvarkyklės kodas let arr=[12, 11 , 13, 5, 6]; tegul N = arr.length;>5 6 11 12 13> The atrankos rūšiavimas algoritmas surūšiuoja masyvą, pakartotinai surasdamas mažiausią elementą (atsižvelgiant į didėjančią tvarką) iš nerūšiuotos dalies ir įtraukdamas jį į pradžią. Algoritmas tam tikrame masyve palaiko dvi pogrupes.
- Pogrupis jau surūšiuotas.
- Likęs pogrupis nerūšiuotas.
Kiekvienoje atrankos rūšiavimo iteracijoje minimalus elementas (atsižvelgiant į didėjančią tvarką) iš nerūšiuoto poskirčio yra parenkamas ir perkeliamas į surūšiuotą pogrupį.
Toliau pateikiamas pavyzdys, paaiškinantis aukščiau nurodytus veiksmus:
arr[] = 64 25 12 22 11 // Find the minimum element in arr[0...4] // and place it at beginning 11 25 12 22 64 // Find the minimum element in arr[1...4] // and place it at beginning of arr[1...4] 11 12 25 22 64 // Find the minimum element in arr[2...4] // and place it at beginning of arr[2...4] 11 12 22 25 64 // Find the minimum element in arr[3...4] // and place it at beginning of arr[3...4] 11 12 22 25 64>Žemiau yra tos pačios programos:
C++
// C++ program for implementation of>// selection sort>#include>using>namespace>std;>// Function to swap two number>void>swap(>int>* xp,>int>* yp)>{>>int>temp = *xp;>>*xp = *yp;>>*yp = temp;>}>// Function to implement the selection>// sort>void>selectionSort(>int>arr[],>int>n)>{>>int>i, j, min_idx;>>// One by one move boundary of>>// unsorted subarray>>for>(i = 0; i // Find the minimum element // in unsorted array min_idx = i; for (j = i + 1; j if (arr[j] min_idx = j; // Swap the found minimum element // with the first element swap(&arr[min_idx], &arr[i]); } } // Function to print an array void printArray(int arr[], int size) { int i; for (i = 0; i cout << arr[i] << ' '; } cout << endl; } // Driver Code int main() { int arr[] = { 64, 25, 12, 22, 11 }; int n = sizeof(arr) / sizeof(arr[0]); // Function Call selectionSort(arr, n); cout << 'Sorted array: '; // Print the array printArray(arr, n); return 0; }>>>Java
// Java program for implementation of>// selection sort>import>java.util.*;>class>GFG>{>// Function to implement the selection>// sort>static>void>selectionSort(>int>arr[],>int>n)>{>>int>i, j, min_idx;>>// One by one move boundary of>>// unsorted subarray>>for>(i =>0>; i 1; i++) { // Find the minimum element // in unsorted array min_idx = i; for (j = i + 1; j if (arr[j] min_idx = j; // Swap the found minimum element // with the first element int temp = arr[min_idx]; arr[min_idx]= arr[i]; arr[i] = temp; } } // Function to print an array static void printArray(int arr[], int size) { int i; for (i = 0; i System.out.print(arr[i]+ ' '); } System.out.println(); } // Driver Code public static void main(String[] args) { int arr[] = { 64, 25, 12, 22, 11 }; int n = arr.length; // Function Call selectionSort(arr, n); System.out.print('Sorted array: '); // Print the array printArray(arr, n); } } // This code is contributed by aashish1995>>>Python3
# Python3 program for implementation of># selection sort># Function to implement the selection># sort>def>selectionSort(arr, n):>># One by one move boundary of>># unsorted subarray>>for>i>in>range>(n>->1>):>># Find the minimum element>># in unsorted array>>min_idx>=>i>>for>j>in>range>(i>+>1>, n):>>if>(arr[j] min_idx = j # Swap the found minimum element # with the first element arr[min_idx], arr[i] = arr[i], arr[min_idx] # Function to print an array def printArray(arr, size): for i in range(size): print(arr[i], end = ' ') print() # Driver Code if __name__ == '__main__': arr = [64, 25, 12, 22, 11] n = len(arr) # Function Call selectionSort(arr, n) print('Sorted array: ') # Print the array printArray(arr, n) # This code is contributed by ukasp>>>C#
... Java
// C# program for implementation of>// selection sort>using>System;>public>class>GFG>{>// Function to implement the selection>// sort>static>void>selectionSort(>int>[]arr,>int>n)>{>>int>i, j, min_idx;>>// One by one move boundary of>>// unsorted subarray>>for>(i = 0; i { // Find the minimum element // in unsorted array min_idx = i; for (j = i + 1; j if (arr[j] min_idx = j; // Swap the found minimum element // with the first element int temp = arr[min_idx]; arr[min_idx]= arr[i]; arr[i] = temp; } } // Function to print an array static void printArray(int []arr, int size) { int i; for (i = 0; i Console.Write(arr[i]+ ' '); } Console.WriteLine(); } // Driver Code public static void Main(String[] args) { int []arr = { 64, 25, 12, 22, 11 }; int n = arr.Length; // Function Call selectionSort(arr, n); Console.Write('Sorted array: '); // Print the array printArray(arr, n); } } // This code is contributed by gauravrajput1>>>Javascript
>// Javascript program for implementation of>// selection sort>// Function to implement the selection>// sort>function>selectionSort(arr, n)>{>>let i, j, min_idx;>>>// One by one move boundary of>>// unsorted subarray>>for>(i = 0; i { // Find the minimum element // in unsorted array min_idx = i; for(j = i + 1; j if (arr[j] min_idx = j; // Swap the found minimum element // with the first element let temp = arr[min_idx]; arr[min_idx]= arr[i]; arr[i] = temp; } } // Function to print an array function printArray(arr, size) { let i; for(i = 0; i { document.write(arr[i] + ' '); } document.write(' '); } // Driver Code let arr = [ 64, 25, 12, 22, 11 ]; let n = arr.length; // Function Call selectionSort(arr, n); document.write('Sorted array: '); // Print the array printArray(arr, n); // This code is contributed by rag2127>>>Išvestis:Sorted array: 11 12 22 25 64>Skirtumas tarp įterpimo rūšiavimo ir pasirinkimo rūšiavimo lentelėje:
Įterpimo rūšiavimas Pasirinkimas Rūšiuoti 1. Įterpia reikšmę į iš anksto surūšiuotą masyvą, kad surūšiuotų masyvo reikšmių rinkinį. Suranda mažiausią / didžiausią skaičių iš sąrašo ir surūšiuoja jį didėjimo / mažėjimo tvarka. 2. Tai stabilus rūšiavimo algoritmas. Tai nestabilus rūšiavimo algoritmas. 3. Geriausiu atveju laiko sudėtingumas yra Ω(N), kai masyvas jau yra didėjančia tvarka. Jis turi Θ (N2) blogiausiu ir vidutiniu atveju. Geriausiu atveju, blogiausio atvejo ir vidutinės atrankos rūšiavimo sudėtingumas yra Θ (N2). 4. Šiame rūšiavimo algoritme atliktų palyginimo operacijų skaičius yra mažesnis nei atliktas keitimas. Šiame rūšiavimo algoritme atliekamų palyginimo operacijų skaičius yra didesnis nei atliktas keitimas. 5. Tai efektyviau nei atrankos rūšiavimas. Tai mažiau efektyvu nei įterpimo rūšiavimas. 6. Čia elementas yra žinomas iš anksto, ir mes ieškome tinkamos padėties jiems įdėti. Vieta, kur įdėti elementą, anksčiau žinoma, ieškome elemento, kurį norite įterpti toje vietoje. 7. Įterpimo rūšiavimas naudojamas, kai:
- Masyve yra nedidelis elementų skaičius
- Liko surūšiuoti tik kelis elementus
Pasirinkimo rūšiavimas naudojamas, kai
- Nedidelis sąrašas turi būti surūšiuotas
- Keitimo kaina neturi reikšmės
- Visų elementų patikrinimas yra privalomas
- Įrašymo į atmintį kaina yra svarbi kaip „flash“ atmintyje (sukeitimų skaičius yra O(n), palyginti su burbulų rūšiavimo O(n2)
8. Įterpimo rūšiavimas yra adaptyvus, t. y. efektyvus duomenų rinkiniams, kurie jau yra iš esmės surūšiuoti: laiko sudėtingumas yra O (kn) kai kiekvienas įvesties elementas yra ne didesnis kaip k vietomis toliau nuo surūšiuotos padėties Pasirinkimo rūšiavimas yra lyginamasis rūšiavimo algoritmas
