Šiame straipsnyje kalbama apie duomenų šifravimo standartą (DES), istorinį šifravimo algoritmą, žinomą dėl 56 bitų rakto ilgio. Mes tyrinėjame jo veikimą, raktų transformavimo ir šifravimo procesą, paaiškindami jo vaidmenį duomenų saugumui ir pažeidžiamumą šiandienos kontekste.
Kas yra DES?
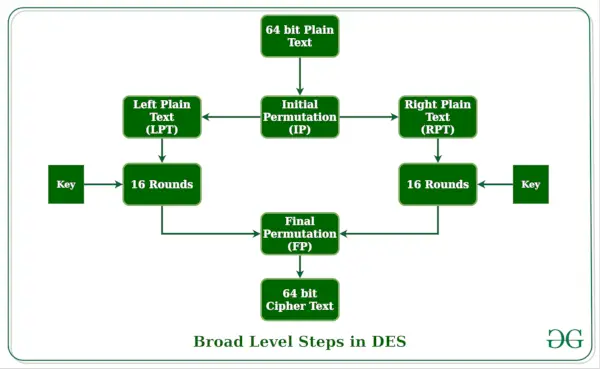
Duomenų šifravimo standartas (DES) yra 56 bitų rakto ilgio blokinis šifras, kuris vaidino svarbų vaidmenį užtikrinant duomenų saugumą. . Duomenų šifravimo standartas (DES) buvo pažeidžiamas labai galingų atakų, todėl DES populiarumas šiek tiek sumažėjo. DES yra blokinis šifras ir užšifruoja duomenis dydžio blokais 64 bitai kiekvienas, o tai reiškia, kad 64 bitai paprasto teksto eina kaip įvestis į DES, kuri sukuria 64 bitus šifruoto teksto. Tas pats algoritmas ir raktas naudojami šifravimui ir iššifravimas , su nedideliais skirtumais. Rakto ilgis yra 56 bitai .
Pagrindinė idėja parodyta žemiau:
Minėjome, kad DES naudoja 56 bitų raktą. Tiesą sakant, pradinis raktas susideda iš 64 bitų. Tačiau dar net neprasidėjus DES procesui, kas 8-as rakto bitas atmetamas, kad būtų sukurtas 56 bitų raktas. Tai reiškia, kad 8, 16, 24, 32, 40, 48, 56 ir 64 bitų pozicijos atmetamos.

Taigi, atmetus kas 8 rakto bitą, gaunamas a 56 bitų raktas nuo originalo 64 bitų raktas .
DES yra pagrįstas dviem pagrindiniais atributais kriptografija : pakeitimas (taip pat vadinamas painiava) ir perkėlimas (taip pat vadinamas difuzija). DES susideda iš 16 žingsnių, kurių kiekvienas vadinamas raundu. Kiekvienas raundas atlieka pakeitimo ir perkėlimo veiksmus. Dabar aptarkime plataus lygio DES veiksmus.
- Pirmajame etape 64 bitų paprasto teksto blokas perduodamas inicialui Permutacija (IP) funkcija.
- Pradinė permutacija atliekama naudojant paprastą tekstą.
- Toliau pradinė permutacija (IP) sukuria dvi permutuoto bloko puses; sakydami kairįjį paprastąjį tekstą (LPT) ir dešinįjį paprastąjį tekstą (RPT).
- Dabar kiekvienas LPT ir RPT pereina 16 šifravimo etapų.
- Galų gale, LPT ir RPT vėl sujungiami ir kombinuotame bloke atliekama galutinė permutacija (FP).
- Šio proceso rezultatas sukuria 64 bitų šifruotą tekstą.
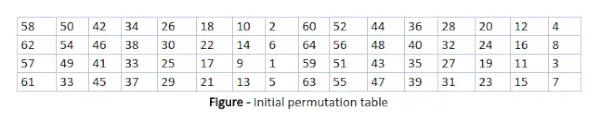
Pradinė permutacija (IP)
Kaip jau pastebėjome, pradinė permutacija (IP) įvyksta tik vieną kartą ir įvyksta prieš pirmąjį raundą. Jame nurodoma, kaip turėtų vykti perkėlimas į IP, kaip parodyta paveikslėlyje. Pavyzdžiui, sakoma, kad IP pakeičia pirmąjį pradinio paprasto teksto bloko bitą 58-uoju originalaus paprastojo teksto bitu, antrąjį - 50-uoju originalaus paprastojo teksto bloko bitu ir pan.
Tai ne kas kita, kaip pradinio paprasto teksto bloko bitų pozicijų žongliravimas. ta pati taisyklė galioja visoms kitoms paveikslėlyje parodytoms bitų pozicijoms.
Kaip pastebėjome baigus IP, gautas 64 bitų permutuotas teksto blokas yra padalintas į du pusblokus. Kiekvienas pusblokas susideda iš 32 bitų, o kiekvienas iš 16 raundų, savo ruožtu, susideda iš plataus lygio žingsnių, nurodytų paveikslėlyje.
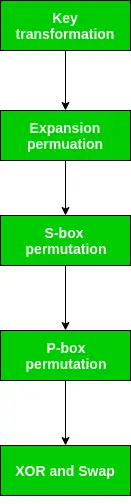
1 veiksmas: rakto transformacija
Pastebėjome, kad pradinis 64 bitų raktas paverčiamas 56 bitų raktu, atmetant kiekvieną 8 pradinio rakto bitą. Taigi kiekvienam yra 56 bitų raktas. Iš šio 56 bitų rakto kiekvieno raundo metu sukuriamas skirtingas 48 bitų antrinis raktas, naudojant procesą, vadinamą rakto transformavimu. Tam 56 bitų raktas yra padalintas į dvi dalis, kurių kiekviena yra po 28 bitus. Šios pusės yra ratu paslinktos į kairę viena arba dviem padėčiais, priklausomai nuo raundo.
Pavyzdžiui: jei apvalūs skaičiai 1, 2, 9 arba 16, kiti raundai perkeliami tik viena padėtimi, apskritimas perkeliamas dviem pozicijomis. Per raundą perstumtų raktų bitų skaičius parodytas paveikslėlyje.

Po atitinkamo poslinkio pasirenkami 48 iš 56 bitų. Iš 48 galime gauti 64 arba 56 bitus pagal reikalavimus, kurie padeda mums suprasti, kad šis modelis yra labai universalus ir gali patenkinti bet kokius reikalingus ar pateiktus reikalavimus. 48 iš 56 bitų pasirinkimui lentelė parodyta toliau pateiktame paveikslėlyje. Pavyzdžiui, po pamainos bitas numeris 14 persikelia į pirmąją padėtį, bitas numeris 17 persikelia į antrąją padėtį ir pan. Jei stebėsime lentelę, suprasime, kad joje yra tik 48 bitų pozicijos. Bitas numeris 18 atmetamas (lentelėje jo nerasime), kaip ir 7 kiti, kad 56 bitų raktas būtų sumažintas į 48 bitų raktą. Kadangi rakto transformavimo procesas apima permutaciją ir pradinio 56 bitų rakto 48 bitų pogrupio pasirinkimą, jis vadinamas suspaudimo permutacija.
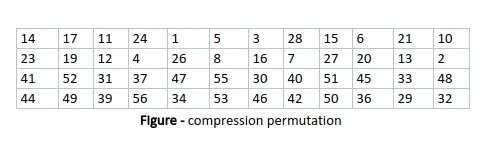
Dėl šios suspaudimo permutacijos technikos kiekviename raunde naudojamas skirtingas raktų bitų poaibis. Dėl to DES nėra lengva nulaužti.
2 veiksmas: išplėtimo permutacija
Prisiminkite, kad po pradinės permutacijos turėjome dvi 32 bitų paprasto teksto sritis, vadinamas kairiuoju paprastu tekstu (LPT) ir dešiniuoju paprastu tekstu (RPT). Išplėtimo permutacijos metu RPT išplečiamas nuo 32 bitų iki 48 bitų. Bitai taip pat permutuojami, todėl vadinami plėtimosi permutacija. Taip atsitinka, kai 32 bitų RPT yra padalintas į 8 blokus, kurių kiekvienas susideda iš 4 bitų. Tada kiekvienas ankstesnio žingsnio 4 bitų blokas išplečiamas iki atitinkamo 6 bitų bloko, t. y. kiekvienam 4 bitų blokui pridedami dar 2 bitai.
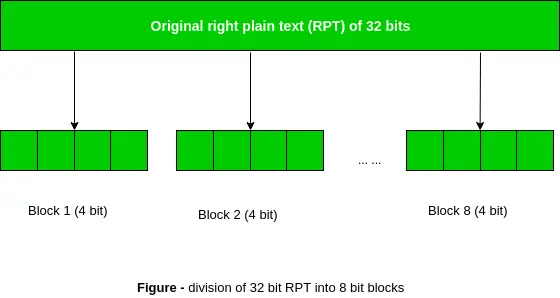
Dėl šio proceso įvesties bitas išplečiamas ir keičiamas kuriant išvestį. Rakto transformavimo procesas suglaudina 56 bitų raktą iki 48 bitų. Tada išplėtimo permutacijos procesas išplečia 32 bitų RPT į 48 bitai . Dabar yra 48 bitų raktas LAISVAS su 48 bitų RPT ir gauta išvestis perduodama kitam žingsniui, kuris yra S-Box pakeitimas .
Python
# Python3 code for the above approach> # Hexadecimal to binary conversion> def> hex2bin(s):> >mp>=> {>'0'>:>'0000'>,> >'1'>:>'0001'>,> >'2'>:>'0010'>,> >'3'>:>'0011'>,> >'4'>:>'0100'>,> >'5'>:>'0101'>,> >'6'>:>'0110'>,> >'7'>:>'0111'>,> >'8'>:>'1000'>,> >'9'>:>'1001'>,> >'A'>:>'1010'>,> >'B'>:>'1011'>,> >'C'>:>'1100'>,> >'D'>:>'1101'>,> >'E'>:>'1110'>,> >'F'>:>'1111'>}> >bin> => ''> >for> i>in> range>(>len>(s)):> >bin> => bin> +> mp[s[i]]> >return> bin> # Binary to hexadecimal conversion> def> bin2hex(s):> >mp>=> {>'0000'>:>'0'>,> >'0001'>:>'1'>,> >'0010'>:>'2'>,> >'0011'>:>'3'>,> >'0100'>:>'4'>,> >'0101'>:>'5'>,> >'0110'>:>'6'>,> >'0111'>:>'7'>,> >'1000'>:>'8'>,> >'1001'>:>'9'>,> >'1010'>:>'A'>,> >'1011'>:>'B'>,> >'1100'>:>'C'>,> >'1101'>:>'D'>,> >'1110'>:>'E'>,> >'1111'>:>'F'>}> >hex> => ''> >for> i>in> range>(>0>,>len>(s),>4>):> >ch>=> ''> >ch>=> ch>+> s[i]> >ch>=> ch>+> s[i>+> 1>]> >ch>=> ch>+> s[i>+> 2>]> >ch>=> ch>+> s[i>+> 3>]> >hex> => hex> +> mp[ch]> >return> hex> # Binary to decimal conversion> def> bin2dec(binary):> >binary1>=> binary> >decimal, i, n>=> 0>,>0>,>0> >while>(binary !>=> 0>):> >dec>=> binary>%> 10> >decimal>=> decimal>+> dec>*> pow>(>2>, i)> >binary>=> binary>/>/>10> >i>+>=> 1> >return> decimal> # Decimal to binary conversion> def> dec2bin(num):> >res>=> bin>(num).replace(>'0b'>, '')> >if>(>len>(res)>%> 4> !>=> 0>):> >div>=> len>(res)>/> 4> >div>=> int>(div)> >counter>=> (>4> *> (div>+> 1>))>-> len>(res)> >for> i>in> range>(>0>, counter):> >res>=> '0'> +> res> >return> res> # Permute function to rearrange the bits> def> permute(k, arr, n):> >permutation>=> ''> >for> i>in> range>(>0>, n):> >permutation>=> permutation>+> k[arr[i]>-> 1>]> >return> permutation> # shifting the bits towards left by nth shifts> def> shift_left(k, nth_shifts):> >s>=> ''> >for> i>in> range>(nth_shifts):> >for> j>in> range>(>1>,>len>(k)):> >s>=> s>+> k[j]> >s>=> s>+> k[>0>]> >k>=> s> >s>=> ''> >return> k> # calculating xow of two strings of binary number a and b> def> xor(a, b):> >ans>=> ''> >for> i>in> range>(>len>(a)):> >if> a[i]>=>=> b[i]:> >ans>=> ans>+> '0'> >else>:> >ans>=> ans>+> '1'> >return> ans> # Table of Position of 64 bits at initial level: Initial Permutation Table> initial_perm>=> [>58>,>50>,>42>,>34>,>26>,>18>,>10>,>2>,> >60>,>52>,>44>,>36>,>28>,>20>,>12>,>4>,> >62>,>54>,>46>,>38>,>30>,>22>,>14>,>6>,> >64>,>56>,>48>,>40>,>32>,>24>,>16>,>8>,> >57>,>49>,>41>,>33>,>25>,>17>,>9>,>1>,> >59>,>51>,>43>,>35>,>27>,>19>,>11>,>3>,> >61>,>53>,>45>,>37>,>29>,>21>,>13>,>5>,> >63>,>55>,>47>,>39>,>31>,>23>,>15>,>7>]> # Expansion D-box Table> exp_d>=> [>32>,>1>,>2>,>3>,>4>,>5>,>4>,>5>,> >6>,>7>,>8>,>9>,>8>,>9>,>10>,>11>,> >12>,>13>,>12>,>13>,>14>,>15>,>16>,>17>,> >16>,>17>,>18>,>19>,>20>,>21>,>20>,>21>,> >22>,>23>,>24>,>25>,>24>,>25>,>26>,>27>,> >28>,>29>,>28>,>29>,>30>,>31>,>32>,>1>]> # Straight Permutation Table> per>=> [>16>,>7>,>20>,>21>,> >29>,>12>,>28>,>17>,> >1>,>15>,>23>,>26>,> >5>,>18>,>31>,>10>,> >2>,>8>,>24>,>14>,> >32>,>27>,>3>,>9>,> >19>,>13>,>30>,>6>,> >22>,>11>,>4>,>25>]> # S-box Table> sbox>=> [[[>14>,>4>,>13>,>1>,>2>,>15>,>11>,>8>,>3>,>10>,>6>,>12>,>5>,>9>,>0>,>7>],> >[>0>,>15>,>7>,>4>,>14>,>2>,>13>,>1>,>10>,>6>,>12>,>11>,>9>,>5>,>3>,>8>],> >[>4>,>1>,>14>,>8>,>13>,>6>,>2>,>11>,>15>,>12>,>9>,>7>,>3>,>10>,>5>,>0>],> >[>15>,>12>,>8>,>2>,>4>,>9>,>1>,>7>,>5>,>11>,>3>,>14>,>10>,>0>,>6>,>13>]],> >[[>15>,>1>,>8>,>14>,>6>,>11>,>3>,>4>,>9>,>7>,>2>,>13>,>12>,>0>,>5>,>10>],> >[>3>,>13>,>4>,>7>,>15>,>2>,>8>,>14>,>12>,>0>,>1>,>10>,>6>,>9>,>11>,>5>],> >[>0>,>14>,>7>,>11>,>10>,>4>,>13>,>1>,>5>,>8>,>12>,>6>,>9>,>3>,>2>,>15>],> >[>13>,>8>,>10>,>1>,>3>,>15>,>4>,>2>,>11>,>6>,>7>,>12>,>0>,>5>,>14>,>9>]],> >[[>10>,>0>,>9>,>14>,>6>,>3>,>15>,>5>,>1>,>13>,>12>,>7>,>11>,>4>,>2>,>8>],> >[>13>,>7>,>0>,>9>,>3>,>4>,>6>,>10>,>2>,>8>,>5>,>14>,>12>,>11>,>15>,>1>],> >[>13>,>6>,>4>,>9>,>8>,>15>,>3>,>0>,>11>,>1>,>2>,>12>,>5>,>10>,>14>,>7>],> >[>1>,>10>,>13>,>0>,>6>,>9>,>8>,>7>,>4>,>15>,>14>,>3>,>11>,>5>,>2>,>12>]],> >[[>7>,>13>,>14>,>3>,>0>,>6>,>9>,>10>,>1>,>2>,>8>,>5>,>11>,>12>,>4>,>15>],> >[>13>,>8>,>11>,>5>,>6>,>15>,>0>,>3>,>4>,>7>,>2>,>12>,>1>,>10>,>14>,>9>],> >[>10>,>6>,>9>,>0>,>12>,>11>,>7>,>13>,>15>,>1>,>3>,>14>,>5>,>2>,>8>,>4>],> >[>3>,>15>,>0>,>6>,>10>,>1>,>13>,>8>,>9>,>4>,>5>,>11>,>12>,>7>,>2>,>14>]],> >[[>2>,>12>,>4>,>1>,>7>,>10>,>11>,>6>,>8>,>5>,>3>,>15>,>13>,>0>,>14>,>9>],> >[>14>,>11>,>2>,>12>,>4>,>7>,>13>,>1>,>5>,>0>,>15>,>10>,>3>,>9>,>8>,>6>],> >[>4>,>2>,>1>,>11>,>10>,>13>,>7>,>8>,>15>,>9>,>12>,>5>,>6>,>3>,>0>,>14>],> >[>11>,>8>,>12>,>7>,>1>,>14>,>2>,>13>,>6>,>15>,>0>,>9>,>10>,>4>,>5>,>3>]],> >[[>12>,>1>,>10>,>15>,>9>,>2>,>6>,>8>,>0>,>13>,>3>,>4>,>14>,>7>,>5>,>11>],> >[>10>,>15>,>4>,>2>,>7>,>12>,>9>,>5>,>6>,>1>,>13>,>14>,>0>,>11>,>3>,>8>],> >[>9>,>14>,>15>,>5>,>2>,>8>,>12>,>3>,>7>,>0>,>4>,>10>,>1>,>13>,>11>,>6>],> >[>4>,>3>,>2>,>12>,>9>,>5>,>15>,>10>,>11>,>14>,>1>,>7>,>6>,>0>,>8>,>13>]],> >[[>4>,>11>,>2>,>14>,>15>,>0>,>8>,>13>,>3>,>12>,>9>,>7>,>5>,>10>,>6>,>1>],> >[>13>,>0>,>11>,>7>,>4>,>9>,>1>,>10>,>14>,>3>,>5>,>12>,>2>,>15>,>8>,>6>],> >[>1>,>4>,>11>,>13>,>12>,>3>,>7>,>14>,>10>,>15>,>6>,>8>,>0>,>5>,>9>,>2>],> >[>6>,>11>,>13>,>8>,>1>,>4>,>10>,>7>,>9>,>5>,>0>,>15>,>14>,>2>,>3>,>12>]],> >[[>13>,>2>,>8>,>4>,>6>,>15>,>11>,>1>,>10>,>9>,>3>,>14>,>5>,>0>,>12>,>7>],> >[>1>,>15>,>13>,>8>,>10>,>3>,>7>,>4>,>12>,>5>,>6>,>11>,>0>,>14>,>9>,>2>],> >[>7>,>11>,>4>,>1>,>9>,>12>,>14>,>2>,>0>,>6>,>10>,>13>,>15>,>3>,>5>,>8>],> >[>2>,>1>,>14>,>7>,>4>,>10>,>8>,>13>,>15>,>12>,>9>,>0>,>3>,>5>,>6>,>11>]]]> # Final Permutation Table> final_perm>=> [>40>,>8>,>48>,>16>,>56>,>24>,>64>,>32>,> >39>,>7>,>47>,>15>,>55>,>23>,>63>,>31>,> >38>,>6>,>46>,>14>,>54>,>22>,>62>,>30>,> >37>,>5>,>45>,>13>,>53>,>21>,>61>,>29>,> >36>,>4>,>44>,>12>,>52>,>20>,>60>,>28>,> >35>,>3>,>43>,>11>,>51>,>19>,>59>,>27>,> >34>,>2>,>42>,>10>,>50>,>18>,>58>,>26>,> >33>,>1>,>41>,>9>,>49>,>17>,>57>,>25>]> def> encrypt(pt, rkb, rk):> >pt>=> hex2bin(pt)> ># Initial Permutation> >pt>=> permute(pt, initial_perm,>64>)> >print>(>'After initial permutation'>, bin2hex(pt))> ># Splitting> >left>=> pt[>0>:>32>]> >right>=> pt[>32>:>64>]> >for> i>in> range>(>0>,>16>):> ># Expansion D-box: Expanding the 32 bits data into 48 bits> >right_expanded>=> permute(right, exp_d,>48>)> ># XOR RoundKey[i] and right_expanded> >xor_x>=> xor(right_expanded, rkb[i])> ># S-boxex: substituting the value from s-box table by calculating row and column> >sbox_str>=> ''> >for> j>in> range>(>0>,>8>):> >row>=> bin2dec(>int>(xor_x[j>*> 6>]>+> xor_x[j>*> 6> +> 5>]))> >col>=> bin2dec(> >int>(xor_x[j>*> 6> +> 1>]>+> xor_x[j>*> 6> +> 2>]>+> xor_x[j>*> 6> +> 3>]>+> xor_x[j>*> 6> +> 4>]))> >val>=> sbox[j][row][col]> >sbox_str>=> sbox_str>+> dec2bin(val)> ># Straight D-box: After substituting rearranging the bits> >sbox_str>=> permute(sbox_str, per,>32>)> ># XOR left and sbox_str> >result>=> xor(left, sbox_str)> >left>=> result> ># Swapper> >if>(i !>=> 15>):> >left, right>=> right, left> >print>(>'Round '>, i>+> 1>,>' '>, bin2hex(left),> >' '>, bin2hex(right),>' '>, rk[i])> ># Combination> >combine>=> left>+> right> ># Final permutation: final rearranging of bits to get cipher text> >cipher_text>=> permute(combine, final_perm,>64>)> >return> cipher_text> pt>=> '123456ABCD132536'> key>=> 'AABB09182736CCDD'> # Key generation> # --hex to binary> key>=> hex2bin(key)> # --parity bit drop table> keyp>=> [>57>,>49>,>41>,>33>,>25>,>17>,>9>,> >1>,>58>,>50>,>42>,>34>,>26>,>18>,> >10>,>2>,>59>,>51>,>43>,>35>,>27>,> >19>,>11>,>3>,>60>,>52>,>44>,>36>,> >63>,>55>,>47>,>39>,>31>,>23>,>15>,> >7>,>62>,>54>,>46>,>38>,>30>,>22>,> >14>,>6>,>61>,>53>,>45>,>37>,>29>,> >21>,>13>,>5>,>28>,>20>,>12>,>4>]> # getting 56 bit key from 64 bit using the parity bits> key>=> permute(key, keyp,>56>)> # Number of bit shifts> shift_table>=> [>1>,>1>,>2>,>2>,> >2>,>2>,>2>,>2>,> >1>,>2>,>2>,>2>,> >2>,>2>,>2>,>1>]> # Key- Compression Table : Compression of key from 56 bits to 48 bits> key_comp>=> [>14>,>17>,>11>,>24>,>1>,>5>,> >3>,>28>,>15>,>6>,>21>,>10>,> >23>,>19>,>12>,>4>,>26>,>8>,> >16>,>7>,>27>,>20>,>13>,>2>,> >41>,>52>,>31>,>37>,>47>,>55>,> >30>,>40>,>51>,>45>,>33>,>48>,> >44>,>49>,>39>,>56>,>34>,>53>,> >46>,>42>,>50>,>36>,>29>,>32>]> # Splitting> left>=> key[>0>:>28>]># rkb for RoundKeys in binary> right>=> key[>28>:>56>]># rk for RoundKeys in hexadecimal> rkb>=> []> rk>=> []> for> i>in> range>(>0>,>16>):> ># Shifting the bits by nth shifts by checking from shift table> >left>=> shift_left(left, shift_table[i])> >right>=> shift_left(right, shift_table[i])> ># Combination of left and right string> >combine_str>=> left>+> right> ># Compression of key from 56 to 48 bits> >round_key>=> permute(combine_str, key_comp,>48>)> >rkb.append(round_key)> >rk.append(bin2hex(round_key))> print>(>'Encryption'>)> cipher_text>=> bin2hex(encrypt(pt, rkb, rk))> print>(>'Cipher Text : '>, cipher_text)> print>(>'Decryption'>)> rkb_rev>=> rkb[::>->1>]> rk_rev>=> rk[::>->1>]> text>=> bin2hex(encrypt(cipher_text, rkb_rev, rk_rev))> print>(>'Plain Text : '>, text)> # This code is contributed by Aditya Jain> |
>
>
Javascript
// Define DES key and plaintext> const key =>'0123456789abcdef'>;> const plaintext =>'Hello, world!'>;> // Perform DES encryption> const des =>new> DES(key);> const ciphertext = des.encrypt(plaintext);> // Perform DES decryption> const decrypted = des.decrypt(ciphertext);> // Print results> console.log(>'Plaintext: '>, plaintext);> console.log(>'Ciphertext: '>, ciphertext);> console.log(>'Decrypted: '>, decrypted);> // Define DES class> class DES {> >constructor(key) {> >// Initialize DES with key> >this>.key = CryptoJS.enc.Hex.parse(key);> >}> >encrypt(plaintext) {> >// Perform DES encryption on plaintext> >const encrypted = CryptoJS.DES.encrypt(> >plaintext,> >this>.key,> >{ mode: CryptoJS.mode.ECB }> >);> >// Return ciphertext as hex string> >return> encrypted.ciphertext.toString();> >}> >decrypt(ciphertext) {> >// Parse ciphertext from hex string> >const ciphertextHex = CryptoJS.enc.Hex.parse(ciphertext);> >// Perform DES decryption on ciphertext> >const decrypted = CryptoJS.DES.decrypt(> >{ ciphertext: ciphertextHex },> >this>.key,> >{ mode: CryptoJS.mode.ECB }> >);> >// Return decrypted plaintext as UTF-8 string> >return> decrypted.toString(CryptoJS.enc.Utf8);> >}> }> |
>
>Išvestis
oi sąvokos
...60AF7CA5 Round 12 FF3C485F 22A5963B C2C1E96A4BF3 Round 13 22A5963B 387CCDAA 99C31397C91F Round 14 387CCDAA BD2DD2AB 251B8BC717D0 Round 15 BD2DD2AB CF26B472 3330C5D9A36D Round 16 19BA9212 CF26B472 181C5D75C66D Cipher Text: C0B7A8D05F3A829C Decryption After initial permutation: 19BA9212CF26B472 After splitting: L0=19BA9212 R0=CF26B472 Round 1 CF26B472 BD2DD2AB 181C5D75C66D Round 2 BD2DD2AB 387CCDAA 3330C5D9A36D Round 3 387CCDAA 22A5963B 251B8BC717D0 Round 4 22A5963B FF3C485F 99C31397C91F Round 5 FF3C485F 6CA6CB20 C2C1E96A4BF3 Round 6 6CA6CB20 10AF9D37 6D5560AF7CA5 Round 7 10AF9D37 308BEE97 02765708B5BF Round 8 308BEE97 A9FC20A3 84BB4473DCCC Round 9 A9FC20A3 2E8F9C65 34F822F0C66D Round 10 2E8F9C65 A15A4B87 708AD2DDB3C0 Round 11 A15A4B87 236779C2 C1948E87475E Round 12 236779C2 B8089591 69A629FEC913 Round 13 B8089591 4A1210F6 DA2D032B6EE3 Round 14 4A1210F6 5A78E394 06EDA4ACF5B5 Round 15 5A78E394 18CA18AD 4568581ABCCE Round 16 14A7D678 18CA18AD 194CD072DE8C Plain Text: 123456ABCD132536>
Išvestis:
Encryption: After initial permutation: 14A7D67818CA18AD After splitting: L0=14A7D678 R0=18CA18AD Round 1 18CA18AD 5A78E394 194CD072DE8C Round 2 5A78E394 4A1210F6 4568581ABCCE Round 3 4A1210F6 B8089591 06EDA4ACF5B5 Round 4 B8089591 236779C2 DA2D032B6EE3 Round 5 236779C2 A15A4B87 69A629FEC913 Round 6 A15A4B87 2E8F9C65 C1948E87475E Round 7 2E8F9C65 A9FC20A3 708AD2DDB3C0 Round 8 A9FC20A3 308BEE97 34F822F0C66D Round 9 308BEE97 10AF9D37 84BB4473DCCC Round 10 10AF9D37 6CA6CB20 02765708B5BF Round 11 6CA6CB20 FF3C485F 6D5560AF7CA5 Round 12 FF3C485F 22A5963B C2C1E96A4BF3 Round 13 22A5963B 387CCDAA 99C31397C91F Round 14 387CCDAA BD2DD2AB 251B8BC717D0 Round 15 BD2DD2AB CF26B472 3330C5D9A36D Round 16 19BA9212 CF26B472 181C5D75C66D Cipher Text: C0B7A8D05F3A829C Decryption After initial permutation: 19BA9212CF26B472 After splitting: L0=19BA9212 R0=CF26B472 Round 1 CF26B472 BD2DD2AB 181C5D75C66D Round 2 BD2DD2AB 387CCDAA 3330C5D9A36D Round 3 387CCDAA 22A5963B 251B8BC717D0 Round 4 22A5963B FF3C485F 99C31397C91F Round 5 FF3C485F 6CA6CB20 C2C1E96A4BF3 Round 6 6CA6CB20 10AF9D37 6D5560AF7CA5 Round 7 10AF9D37 308BEE97 02765708B5BF Round 8 308BEE97 A9FC20A3 84BB4473DCCC Round 9 A9FC20A3 2E8F9C65 34F822F0C66D Round 10 2E8F9C65 A15A4B87 708AD2DDB3C0 Round 11 A15A4B87 236779C2 C1948E87475E Round 12 236779C2 B8089591 69A629FEC913 Round 13 B8089591 4A1210F6 DA2D032B6EE3 Round 14 4A1210F6 5A78E394 06EDA4ACF5B5 Round 15 5A78E394 18CA18AD 4568581ABCCE Round 16 14A7D678 18CA18AD 194CD072DE8C Plain Text: 123456ABCD132536>
Išvada
Apibendrinant, duomenų šifravimo standartas (DES) yra a bloko šifras su 56 bitų rakto ilgiu, kuris suvaidino svarbų vaidmenį duomenų saugumui. Tačiau dėl pažeidžiamumo jo populiarumas sumažėjo. DES veikia per daugybę raundų, apimančių raktų transformavimą, išplėtimo permutaciją ir pakeitimą, galiausiai sukuriant šifruotą tekstą iš paprasto teksto. Nors DES turi istorinę reikšmę, labai svarbu apsvarstyti saugesnę šifravimas alternatyvos šiuolaikiniams duomenų apsaugos poreikiams tenkinti.
Dažnai užduodami klausimai
Q.1 : Kas turėtų būti laikoma DES alternatyva duomenų šifravimui?
Atsakymas:
Šiuolaikiniams duomenų šifravimo poreikiams patenkinti apsvarstykite galimybę naudoti stipresnius šifravimo algoritmus, pvz AES (Išplėstinis šifravimo standartas).
Q.2 : Kaip kiekvienam DES etapui generuojamas 48 bitų dalinis raktas?
Atsakymas:
48 bitų dalinis raktas kiekvienam DES etapui yra gaunamas iš 56 bitų rakto per apskrito poslinkio ir permutacijos procesą, užtikrinantį raktų įvairovę.

