NFA gali turėti nulį, vieną ar daugiau nei vieną judesį iš tam tikros būsenos tam tikrame įvesties simbolyje. NFA taip pat gali turėti NULL judesius (judesiai be įvesties simbolio). Kita vertus, DFA turi vieną ir tik vieną judėjimą iš tam tikros būsenos tam tikrame įvesties simbolyje.

NFA konvertavimo į DFA žingsniai:

1 veiksmas: konvertuokite nurodytą NFA į lygiavertę perėjimo lentelę
Norėdami konvertuoti NFA į lygiavertę perėjimo lentelę, turime išvardyti visas būsenas, įvesties simbolius ir perėjimo taisykles. Perėjimo taisyklės vaizduojamos matricos pavidalu, kur eilutės žymi esamą būseną, stulpeliai – įvesties simbolį, o langeliai – kitą būseną.

2 veiksmas: sukurkite DFA pradžios būseną
DFA pradžios būsena yra visų galimų NFA pradinių būsenų rinkinys. Šis rinkinys vadinamas NFA pradžios būsenos uždarymu. Epsilono uždarymas yra visų būsenų, kurias galima pasiekti nuo pradžios būsenos, sekant epsilono (?) perėjimus, rinkinys.

listnode java

3 veiksmas: sukurkite DFA perėjimo lentelę
DFA perėjimo lentelė yra panaši į NFA perėjimo lentelę, tačiau vietoj atskirų būsenų eilutės ir stulpeliai žymi būsenų rinkinius. Kiekvienam įvesties simboliui atitinkamame perėjimo lentelės langelyje yra epsiloninis būsenų rinkinio uždarymas, gautas laikantis perėjimo taisyklių NFA perėjimo lentelėje.

4 veiksmas: sukurkite galutines DFA būsenas
Galutinės DFA būsenos yra būsenų rinkiniai, kuriuose yra bent viena galutinė NFA būsena.

5 veiksmas: supaprastinkite DFA
Ankstesniais žingsniais gautame DFA gali būti nereikalingų būsenų ir perėjimų. Norėdami supaprastinti DFA, galime naudoti šiuos metodus:

Excel datos skirtumas

• Pašalinti nepasiekiamas būsenas: būsenos, kurių negalima pasiekti nuo pradžios būsenos, gali būti pašalintos iš DFA.
• Pašalinti negyvas būsenas: būsenos, kurios negali sukelti galutinės būsenos, gali būti pašalintos iš DFA.
• Sujungti lygiavertes būsenas: būsenos, kurios turi vienodas visų įvesties simbolių perėjimo taisykles, gali būti sujungtos į vieną būseną.

6 veiksmas: kartokite 3–5 veiksmus, kol nebebus įmanoma supaprastinti
Supaprastinę DFA, kartojame 3–5 veiksmus, kol nebebus įmanoma supaprastinti. Galutinis gautas DFA yra sumažintas DFA, atitinkantis nurodytą NFA.

Pavyzdys: Apsvarstykite toliau pateiktą NFA, parodytą 1 paveiksle.

Toliau pateikiami įvairūs NFA parametrai. Q = { q0, q1, q2 } ? = (a, b) F = {q2}? (NFA pereinamoji funkcija)

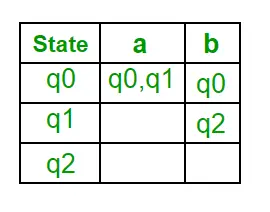
1 veiksmas: Q' = ? 2 veiksmas: Q’ = {q0} 3 veiksmas: raskite kiekvienos Q būsenos būsenas kiekvienam įvesties simboliui. Šiuo metu Q būsena yra q0, raskite perėjimus nuo q0 įvesties simboliuose a ir b naudodami NFA perėjimo funkciją ir atnaujinkite DFA perėjimo lentelę. ?“ (DFA pereinamoji funkcija)

Dabar { q0, q1 } bus laikoma viena būsena. Kadangi jo įrašas nėra Q, pridėkite jį prie Q. Taigi Q' = { q0, { q0, q1 } } Dabar perėjimų iš būsenos { q0, q1 } ant skirtingų įvesties simbolių nėra DFA perėjimo lentelėje, apskaičiuosime taip: ?' ( { q0, q1 } , a ) = ? ( q0, a ) ? ? ( q1, a ) = { q0, q1 } ?’ ( { q0, q1 }, b ) = ? (q0, b) ? ? ( q1, b ) = { q0, q2 } Dabar mes atnaujinsime DFA perėjimo lentelę. ?“ (DFA pereinamoji funkcija)

Python programos pavyzdžiai

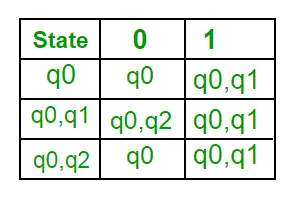
Dabar { q0, q2 } bus laikoma viena būsena. Kadangi jo įrašas nėra Q, pridėkite jį prie Q. Taigi Q' = { q0, { q0, q1 }, { q0, q2 } } Dabar perėjimų iš būsenos {q0, q2} skirtingais įvesties simboliais DFA perėjimo lentelėje nėra, apskaičiuosime taip: ?' ( { q0, q2 }, a ) = ? (q0, a ) ? ? ( q2, a ) = { q0, q1 } ?’ ( { q0, q2 }, b ) = ? (q0, b) ? ? ( q2, b ) = { q0 } Dabar mes atnaujinsime DFA perėjimo lentelę. ?“ (DFA pereinamoji funkcija)

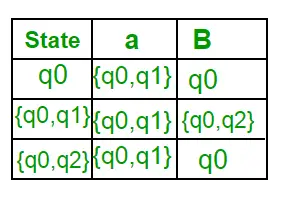
Kadangi naujos būsenos nesukurtos, konvertavimas baigtas. Galutinė DFA būsena bus būsena, kurios komponentas yra q2, t. y. { q0, q2 } Toliau pateikiami įvairūs DFA parametrai. Q’ = {q0, {q0, q1}, {q0, q2}}? = ( a, b ) F = { { q0, q2 } } ir perėjimo funkcija ?', kaip parodyta aukščiau. Galutinė aukščiau pateiktos NFA DFA parodyta 2 paveiksle.

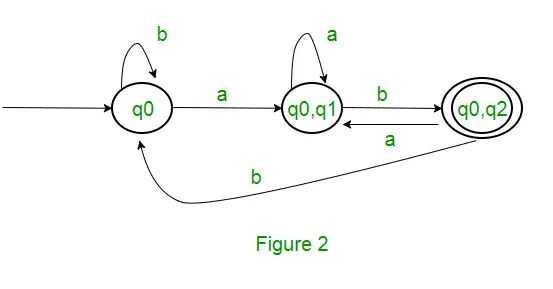
Pastaba: Kartais nelengva reguliariąją išraišką konvertuoti į DFA. Pirmiausia galite konvertuoti įprastą reiškinį į NFA, o tada NFA į DFA.

Klausimas: Būsenų skaičius minimaliame deterministiniame baigtiniame automate, atitinkančiame reguliariąją išraišką (0 + 1)* (10), yra ____________.

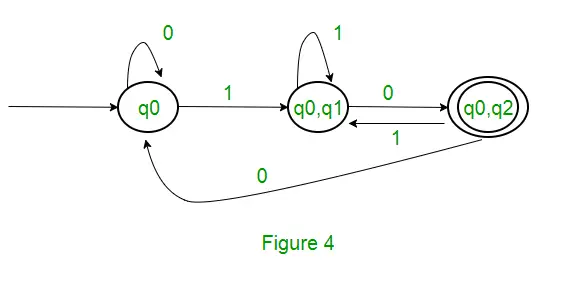
Sprendimas: Pirmiausia sukursime NFA aukščiau nurodytai išraiškai. Norėdami sukurti NFA (0 + 1)*, NFA bus toje pačioje būsenoje q0 su įvesties simboliu 0 arba 1. Tada sujungimui pridėsime du judesius (q0 prie q1, jei 1 ir q1 prie q2, jei 0), kaip parodyta. 3 paveiksle.

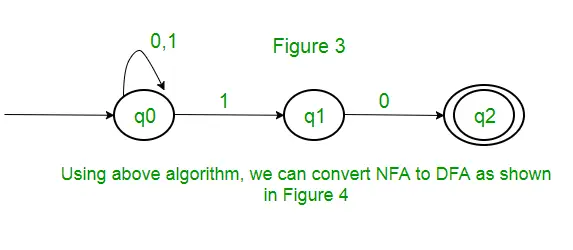
Prie šio straipsnio parengė Sonal Tuteja.